Coordinate Geometry
... As you can see from the figure, each of the points on the coordinate plane receives a pair of coordinates: (x,y) . The first coordinate in a coordinate pair is called the x coordinate. The x coordinate of a point is its location along the x axis and can be determined by the point’s distance from ...
... As you can see from the figure, each of the points on the coordinate plane receives a pair of coordinates: (x,y) . The first coordinate in a coordinate pair is called the x coordinate. The x coordinate of a point is its location along the x axis and can be determined by the point’s distance from ...
O`Neill`s Math
... circumference, area, volume, lateral area, and surface area of common geometric figures. 16.0 Perform basic constructions with a straightedge and compass, such as angle bisectors, perpendicular bisectors, and the line parallel to a given line through a point off the line. 22.0 Know the effects of ri ...
... circumference, area, volume, lateral area, and surface area of common geometric figures. 16.0 Perform basic constructions with a straightedge and compass, such as angle bisectors, perpendicular bisectors, and the line parallel to a given line through a point off the line. 22.0 Know the effects of ri ...
Wizard Test Maker
... (1) If the corresponding angles of two lines cut by a transversal are equal, the lines are parallel. (2) If two nonparallel lines are cut by a transversal, the corresponding angles are not equal. (3) If the corresponding angles of two lines cut by a transversal are not equal, the lines are not paral ...
... (1) If the corresponding angles of two lines cut by a transversal are equal, the lines are parallel. (2) If two nonparallel lines are cut by a transversal, the corresponding angles are not equal. (3) If the corresponding angles of two lines cut by a transversal are not equal, the lines are not paral ...
Common Core Learning Standards GRADE 7 Mathematics
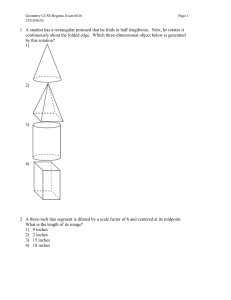
... Define two-dimensional figures that result from slicing a right rectangular prism. Define two-dimensional figures that result from slicing a right rectangular pyramid. Define two-dimensional figures that result from slicing a triangular pyramid. Define two-dimensional figures that result from slicin ...
... Define two-dimensional figures that result from slicing a right rectangular prism. Define two-dimensional figures that result from slicing a right rectangular pyramid. Define two-dimensional figures that result from slicing a triangular pyramid. Define two-dimensional figures that result from slicin ...
Transformation geometry
... This module has an introductory section designed for learners who have not studied isometric transformations (translation, rotation and reflection) at the primary school. Learners who have completed these activities should be able to transform geometric figures as well as recognise given transformat ...
... This module has an introductory section designed for learners who have not studied isometric transformations (translation, rotation and reflection) at the primary school. Learners who have completed these activities should be able to transform geometric figures as well as recognise given transformat ...
Pythagorean Theorem - hrsbstaff.ednet.ns.ca
... 9) Did Pythagoras himself prove the theorem? What was common In this practice at this time? section you will learn about a powerful formula for ...
... 9) Did Pythagoras himself prove the theorem? What was common In this practice at this time? section you will learn about a powerful formula for ...
0002_hsm11gmtr_0201.indd
... transversal intersects parallel lines, special supplementary and congruent angle pairs are formed. Supplementary angles formed by a transversal intersecting parallel lines: same-side interior angles (Postulate 3-1) ...
... transversal intersects parallel lines, special supplementary and congruent angle pairs are formed. Supplementary angles formed by a transversal intersecting parallel lines: same-side interior angles (Postulate 3-1) ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)