Principles of Mathematics, Grade 10, Academic (MPM2D)
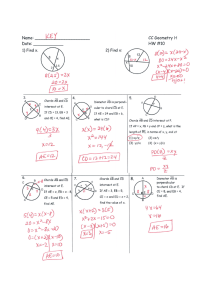
... determine the equation for a circle having centre (0, 0) and radius r, by applying the formula for the length of a line segment; identify the radius of a circle of centre (0, 0), given its equation; and write the equation, given the radius solve multi-step problems, using the concepts of the slope, ...
... determine the equation for a circle having centre (0, 0) and radius r, by applying the formula for the length of a line segment; identify the radius of a circle of centre (0, 0), given its equation; and write the equation, given the radius solve multi-step problems, using the concepts of the slope, ...
3.4 Angles of a Triangle
... The proof uses an auxiliary line. This is a line that is added to the diagram to help in the proof. ...
... The proof uses an auxiliary line. This is a line that is added to the diagram to help in the proof. ...
Educate. Inspire. Empower. Day Essential Question and CCSS
... Extension and application of skills from the week. ...
... Extension and application of skills from the week. ...
Task #2 – Constructing the Circumscribed Circle of a Triangle
... 1. Construct the perpendicular bisector of AC . Label this line n. By the Perpendicular Bisector Theorem, every point on line n is equidistant from A and C. 2. Construct the perpendicular bisector of BC . Label this line m. By the Perpendicular Bisector Theorem, every point on line m is equidistant ...
... 1. Construct the perpendicular bisector of AC . Label this line n. By the Perpendicular Bisector Theorem, every point on line n is equidistant from A and C. 2. Construct the perpendicular bisector of BC . Label this line m. By the Perpendicular Bisector Theorem, every point on line m is equidistant ...
ASA and SAS Postulates - Clark Magnet High School
... We don’t need to get expert advice to prove this is true. We can all agree that there is only one straight line that exists between two points. Because it is something we can all agree on, it is known as a postulate. ...
... We don’t need to get expert advice to prove this is true. We can all agree that there is only one straight line that exists between two points. Because it is something we can all agree on, it is known as a postulate. ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)