Thales of Miletus1 - Department of Mathematics
... thus, his achievements are difficult to assess, particularly his philosophy and mathematical discoveries. Indeed, many mathematical discoveries of this early period have been attributed to others, often centuries later. In addition one must consider the ancient practice of crediting particular disco ...
... thus, his achievements are difficult to assess, particularly his philosophy and mathematical discoveries. Indeed, many mathematical discoveries of this early period have been attributed to others, often centuries later. In addition one must consider the ancient practice of crediting particular disco ...
Show all work on a separate sheet of work paper
... Find the area of a circle whose circumference is 6π cm. Leave your answer in terms of π. Find the area of a circle whose circumference is 8π cm. Leave your answer in terms of π. Find the area of a circle whose circumference is 10π cm. Leave your answer in terms of π. Find the area of a circle whose ...
... Find the area of a circle whose circumference is 6π cm. Leave your answer in terms of π. Find the area of a circle whose circumference is 8π cm. Leave your answer in terms of π. Find the area of a circle whose circumference is 10π cm. Leave your answer in terms of π. Find the area of a circle whose ...
Foundations of Geometry
... euclidean geometry may be developed without the use of the axiom of continuity; the significance of Desargues’s theorem, as a condition that a given plane geometry may be regarded as a part of a geometry of space, is made apparent, etc. 5. A variety of algebras of segments are introduced in accordan ...
... euclidean geometry may be developed without the use of the axiom of continuity; the significance of Desargues’s theorem, as a condition that a given plane geometry may be regarded as a part of a geometry of space, is made apparent, etc. 5. A variety of algebras of segments are introduced in accordan ...
SYLLABUS FOR PRIMARY SCHOOL MATHEMATICS General Points for Text Book Writers
... 1. The following syllabus has been developed keeping the philosophy of the Yashpal Report and the National Focus Group for Teaching Learning Mathematics in view. Keeping in mind the reality of the number of hours that teaching actually takes place in the school, we have kept a thumb rule of 140 peri ...
... 1. The following syllabus has been developed keeping the philosophy of the Yashpal Report and the National Focus Group for Teaching Learning Mathematics in view. Keeping in mind the reality of the number of hours that teaching actually takes place in the school, we have kept a thumb rule of 140 peri ...
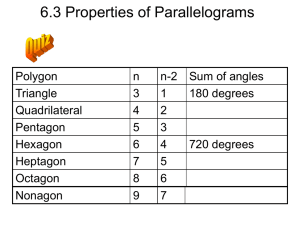
Polygons
... c. A 20-gon, also called an icosagon, is __________ that ___________. d. An equilateral polygon is __________ that ___________. 12. Name a pair of consecutive angles and a pair of consecutive sides in the figure at right. 13. Draw a concave hexagon. How many diagonals does it have? 14. Name the diag ...
... c. A 20-gon, also called an icosagon, is __________ that ___________. d. An equilateral polygon is __________ that ___________. 12. Name a pair of consecutive angles and a pair of consecutive sides in the figure at right. 13. Draw a concave hexagon. How many diagonals does it have? 14. Name the diag ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)