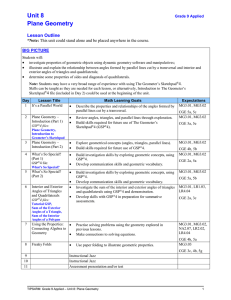
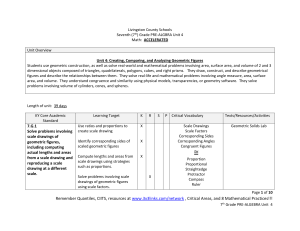
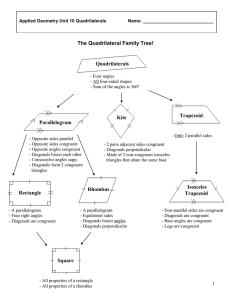
Integrated Geometry - Calendar of Lessons
... 3. explore, using compass and straight edge construction techniques, and conjecture the postulates SAS, ASA, SSS for proving triangles congruent (i.e. If two triangles agree in three sides, then these triangles are congruent.) 4. draw diagrams to illustrate the corresponding sides and angles that ne ...
... 3. explore, using compass and straight edge construction techniques, and conjecture the postulates SAS, ASA, SSS for proving triangles congruent (i.e. If two triangles agree in three sides, then these triangles are congruent.) 4. draw diagrams to illustrate the corresponding sides and angles that ne ...
MATH 113 Section 8.2: Two-Dimensional Figures
... are congruent. That means corresponding sides have the same length, and corresponding angles have the same measure. Example Suppose two triangles, 4ABC and 4XYZ , are congruent. what does this mean about the line segments and angle measures of these triangles? Congruence in Triangles In your lab we ...
... are congruent. That means corresponding sides have the same length, and corresponding angles have the same measure. Example Suppose two triangles, 4ABC and 4XYZ , are congruent. what does this mean about the line segments and angle measures of these triangles? Congruence in Triangles In your lab we ...
Leaving Certificate Mathematics
... Mathematics at Ordinary level is geared to the needs of learners who are beginning to deal with abstract ideas. However, many of them may go on to use and apply mathematics in their future careers, and all of them will meet the subject to a greater or lesser degree in their daily lives. Ordinary lev ...
... Mathematics at Ordinary level is geared to the needs of learners who are beginning to deal with abstract ideas. However, many of them may go on to use and apply mathematics in their future careers, and all of them will meet the subject to a greater or lesser degree in their daily lives. Ordinary lev ...
TO CONSTRUCT AN ANGLE CONGRUENT TO A GIVEN ANGLE
... (do ONE of he above) AND 2 adjacent sides (distances 2x) ...
... (do ONE of he above) AND 2 adjacent sides (distances 2x) ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)