Geometry Unit 9 Test - Quadrilaterals
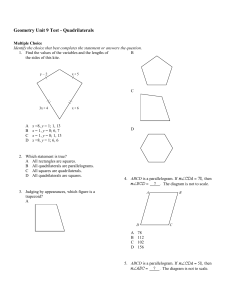
... 17. The isosceles trapezoid is part of an isosceles triangle with a 22° vertex angle. What is the measure of an acute base angle of the trapezoid? Of an obtuse base angle? The diagram is not to scale. ...
... 17. The isosceles trapezoid is part of an isosceles triangle with a 22° vertex angle. What is the measure of an acute base angle of the trapezoid? Of an obtuse base angle? The diagram is not to scale. ...
lesson plan 10-20
... isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. MCC9-12.G.CO.11 Prove theorems about parallelograms. Theorems include: opposite sides are congruent, opposite angl ...
... isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. MCC9-12.G.CO.11 Prove theorems about parallelograms. Theorems include: opposite sides are congruent, opposite angl ...
10 20 lesson plans
... MCC9-12.G.SRT.1 Verify experimentally the properties of dilations given by a center and a scale factor: MCC9-12.G.SRT.2 Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of si ...
... MCC9-12.G.SRT.1 Verify experimentally the properties of dilations given by a center and a scale factor: MCC9-12.G.SRT.2 Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of si ...
Math Background - Connected Mathematics Project
... In Grade 6, area and perimeter were introduced to develop the ideas of measurement around and within polygons in Covering and Surrounding. This Unit focuses on polygons beyond triangles and quadrilaterals, developing the relationships between sides and angles. These relationships lead to such ideas ...
... In Grade 6, area and perimeter were introduced to develop the ideas of measurement around and within polygons in Covering and Surrounding. This Unit focuses on polygons beyond triangles and quadrilaterals, developing the relationships between sides and angles. These relationships lead to such ideas ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)