The Postulates of Neutral Geometry Axiom 1 (The Set Postulate
... P lies on the bisector of ∠AOB if and only if it is equidistant from OA and OB. Theorem 6.11 (Alternate Interior Angles Theorem). If two lines are cut by a transversal making a pair of congruent alternate interior angles, then they are parallel. Corollary 6.12 (Corresponding Angles Theorem). If two ...
... P lies on the bisector of ∠AOB if and only if it is equidistant from OA and OB. Theorem 6.11 (Alternate Interior Angles Theorem). If two lines are cut by a transversal making a pair of congruent alternate interior angles, then they are parallel. Corollary 6.12 (Corresponding Angles Theorem). If two ...
Chapter10
... In lesson 1-6, you found the areas of rectangles. For any polygon and a given unit of measure, there is a ...
... In lesson 1-6, you found the areas of rectangles. For any polygon and a given unit of measure, there is a ...
4 notes - Blackboard
... BC ! EF Prove: ∆ ABC ≅ ∆ DEF A Proof: “see paragraph form with key steps” ...
... BC ! EF Prove: ∆ ABC ≅ ∆ DEF A Proof: “see paragraph form with key steps” ...
Chapter 2 Angles
... using a protractor to construct an angle of a given size and to measure angles estimating and measuring angles in ...
... using a protractor to construct an angle of a given size and to measure angles estimating and measuring angles in ...
kucukarslan et al.
... Fuzzy sets theory was introduced by Zadeh in 1965. A fuzzy set is characterized by a membership function which assigns to each object a grade of membership ranging between zero and one. One of the main goals in the fuzzy sets theory is to give fuzzification of different classical mathematical struct ...
... Fuzzy sets theory was introduced by Zadeh in 1965. A fuzzy set is characterized by a membership function which assigns to each object a grade of membership ranging between zero and one. One of the main goals in the fuzzy sets theory is to give fuzzification of different classical mathematical struct ...
pdf Version
... He makes use of repeated dissections [6]. As a consequence of a theorem proved by Max Dehn in 1900 that any proof of the volume of a pyramid must use infinitesimal considerations in one form or another, Liu Hui does in fact use a limit process [6]! It is amazing that he considered these methods by h ...
... He makes use of repeated dissections [6]. As a consequence of a theorem proved by Max Dehn in 1900 that any proof of the volume of a pyramid must use infinitesimal considerations in one form or another, Liu Hui does in fact use a limit process [6]! It is amazing that he considered these methods by h ...
Chapter 4 Notes
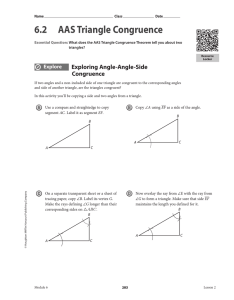
... Postulate - ASA – If two angles and the included side of one triangle are congruent to the corresponding two angles and the included side of another triangle, then the two triangles are congruent. Theorem - AAS – If two angles and a nonincluded side of one triangle are congruent to the corresponding ...
... Postulate - ASA – If two angles and the included side of one triangle are congruent to the corresponding two angles and the included side of another triangle, then the two triangles are congruent. Theorem - AAS – If two angles and a nonincluded side of one triangle are congruent to the corresponding ...
Proving that a quadrilateral is a Parallelogram
... --Both pairs of opposite sides are parallel (definition) --One pair of opposite sides is both congruent and parallel --Both pairs of opposite sides are congruent --Both pairs of opposite angles are congruent --One angle is supplementary to both of its consecutive angles --Both diagonals bisect each ...
... --Both pairs of opposite sides are parallel (definition) --One pair of opposite sides is both congruent and parallel --Both pairs of opposite sides are congruent --Both pairs of opposite angles are congruent --One angle is supplementary to both of its consecutive angles --Both diagonals bisect each ...
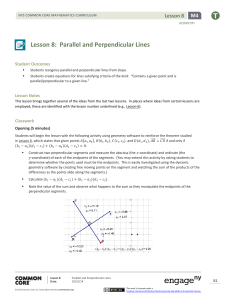
Chapter 3 – Parallel and Perpendicular Lines
... Summarize the method for algebraically finding the distance between two lines 1. Find the slope of the parallel linesFind the slope of a perpendicular line. 2. Find the equation of a perpendicular line. (Use the perpendicular slope and choose a point on one of the two parallel lines) 3. Use a syste ...
... Summarize the method for algebraically finding the distance between two lines 1. Find the slope of the parallel linesFind the slope of a perpendicular line. 2. Find the equation of a perpendicular line. (Use the perpendicular slope and choose a point on one of the two parallel lines) 3. Use a syste ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)