Student Learning Map Unit 3
... the interior and exterior angles all have the same measure. For the pentagon, there are 5 interior and exterior angles. The sum of the exterior angles is 360° and the sum of the interior angles is 540°. Each exterior angle: 360°/5 = 72° Each interior angle: 540°/5=108° For the hexagon, there are 6 i ...
... the interior and exterior angles all have the same measure. For the pentagon, there are 5 interior and exterior angles. The sum of the exterior angles is 360° and the sum of the interior angles is 540°. Each exterior angle: 360°/5 = 72° Each interior angle: 540°/5=108° For the hexagon, there are 6 i ...
Discovering Properties of Parallelograms
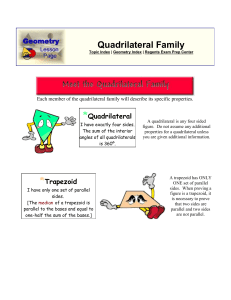
... If two parallel lines are intersected by a second pair of parallel lines the same distance apart as the first pair, then the parallelogram formed is a rhombus. ...
... If two parallel lines are intersected by a second pair of parallel lines the same distance apart as the first pair, then the parallelogram formed is a rhombus. ...
Unit 4 Geometry: Angles and Areas
... Technology: dynamic geometry software. Students are expected to use dynamic geometry software to draw geometric shapes. Most activities in this unit use a program called The Geometer’s Sketchpad®, and some are instructional—they help you teach students how to use the program. If you are not familiar ...
... Technology: dynamic geometry software. Students are expected to use dynamic geometry software to draw geometric shapes. Most activities in this unit use a program called The Geometer’s Sketchpad®, and some are instructional—they help you teach students how to use the program. If you are not familiar ...
Revised Version 070216
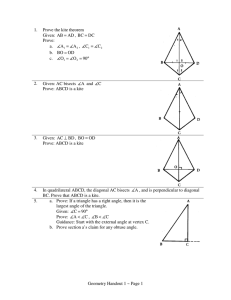
... Thus point C must be on circle K, and quadrilateral ABCD is inscribed in circle K. In this way, the center of circumcircle K will be the circumcenter of triangle ABD, triangle BCD, and quadrilateral ABCD. Therefore, the point of concurrence of the perpendicular bisectors of AB,BC,CD, and AD will be ...
... Thus point C must be on circle K, and quadrilateral ABCD is inscribed in circle K. In this way, the center of circumcircle K will be the circumcenter of triangle ABD, triangle BCD, and quadrilateral ABCD. Therefore, the point of concurrence of the perpendicular bisectors of AB,BC,CD, and AD will be ...
Fall Geometry Final Review Answer Section
... 2. Write the two conditional statements that make up the following biconditional. I drink juice if (and only if) it is breakfast time. 3. Is the following definition of dog reversible? If yes, write it as a true biconditional. A dog is a mammal. 4. One way to show that a statement is NOT a good defi ...
... 2. Write the two conditional statements that make up the following biconditional. I drink juice if (and only if) it is breakfast time. 3. Is the following definition of dog reversible? If yes, write it as a true biconditional. A dog is a mammal. 4. One way to show that a statement is NOT a good defi ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)