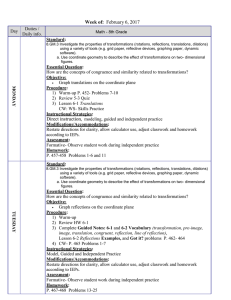
Overview - Windham Math
... good definition, conjecture, counterexample, bi-conditional, conditional statement, converse, informal proof, counterexample, deductive, inductive, reasoning, construction, point, line, plane, collinear, coplanar, intersecting, segment, ray, opposite rays, angle, acute angle, right angle, obtuse ang ...
... good definition, conjecture, counterexample, bi-conditional, conditional statement, converse, informal proof, counterexample, deductive, inductive, reasoning, construction, point, line, plane, collinear, coplanar, intersecting, segment, ray, opposite rays, angle, acute angle, right angle, obtuse ang ...
Special Right Triangles
... lengths of an isosceles right triangle: 1 − 1 − 2 Now we take notice of the angle measures. Since the diagonal of a square bisects the angles (which were originally 90 D ), each of the angles in the triangle is 45D . Using the idea of proportion and similar triangles, we ...
... lengths of an isosceles right triangle: 1 − 1 − 2 Now we take notice of the angle measures. Since the diagonal of a square bisects the angles (which were originally 90 D ), each of the angles in the triangle is 45D . Using the idea of proportion and similar triangles, we ...
Core III Homework Week of 2/25/13
... Core III Homework Week of 2/25/13 p.408/3,5,7 Plus Reteach-Intervention Sheets ...
... Core III Homework Week of 2/25/13 p.408/3,5,7 Plus Reteach-Intervention Sheets ...
Triangle Congruence
... In triangle ABC, the measure of angle B is twice the measure of angle A and an exterior angle at vertex C measures 120o. Find the measure of angle A. ...
... In triangle ABC, the measure of angle B is twice the measure of angle A and an exterior angle at vertex C measures 120o. Find the measure of angle A. ...
Name - West Ada
... The Pythagorean Theorem can be used to find the length of a side of a right triangle. Pythagorean Theorem: a2 + b2 = c2, where a and b are the legs of a right triangle, and c is the hypotenuse. ...
... The Pythagorean Theorem can be used to find the length of a side of a right triangle. Pythagorean Theorem: a2 + b2 = c2, where a and b are the legs of a right triangle, and c is the hypotenuse. ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)