Converse of the Pythagorean Theorem
... Provide instruction on writing mathematical explanations, justifications, and proofs. Encourage the student to first consider the statement to be proven. Next, ask the student to examine the assumptions and then formulate an overall strategy. Make clear that every step must be justified with mathema ...
... Provide instruction on writing mathematical explanations, justifications, and proofs. Encourage the student to first consider the statement to be proven. Next, ask the student to examine the assumptions and then formulate an overall strategy. Make clear that every step must be justified with mathema ...
Lecture 8 - CSUN.edu
... Construct a triangle if three sides are given Construct a triangle if two sides and angle between them are given Construct a triangle if one side and two angles on that side are given Proofs for symmetry explanations o Theorem 1 : In an isosceles triangle, base angles are congruent. o Theorem 2 : If ...
... Construct a triangle if three sides are given Construct a triangle if two sides and angle between them are given Construct a triangle if one side and two angles on that side are given Proofs for symmetry explanations o Theorem 1 : In an isosceles triangle, base angles are congruent. o Theorem 2 : If ...
Date - Garnet Valley School District
... In 2004, several nickels were minted to commemorate the Louisiana Purchase and Lewis and Clark’s expedition into the American West. One nickel shows a pipe and a hatchet crossed to symbolize peace between the American government and Native American tribes. 6. Name a pair of vertical angles. ...
... In 2004, several nickels were minted to commemorate the Louisiana Purchase and Lewis and Clark’s expedition into the American West. One nickel shows a pipe and a hatchet crossed to symbolize peace between the American government and Native American tribes. 6. Name a pair of vertical angles. ...
Converse of the Pythagorean Theorem
... Provide instruction on writing mathematical explanations, justifications, and proofs. Encourage the student to first consider the statement to be proven. Next, ask the student to examine the assumptions and then formulate an overall strategy. Make clear that every step must be justified with mathema ...
... Provide instruction on writing mathematical explanations, justifications, and proofs. Encourage the student to first consider the statement to be proven. Next, ask the student to examine the assumptions and then formulate an overall strategy. Make clear that every step must be justified with mathema ...
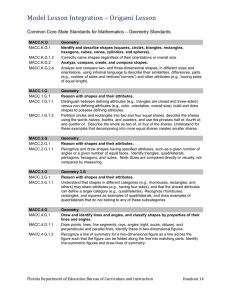
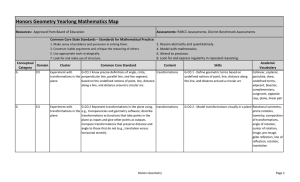
Honors Geometry Yearlong Curriculum Map
... congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. G-CO.11 Prove theorems about parallelograms. Theorems include: opposite sides are congruent, opposite angles are congruent, the diagonals ...
... congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. G-CO.11 Prove theorems about parallelograms. Theorems include: opposite sides are congruent, opposite angles are congruent, the diagonals ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)