Computational Problem of the Determinant Matrix Calculation
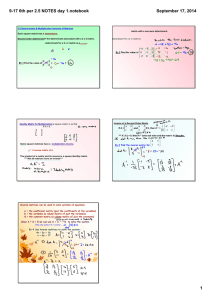
... The determinant of matrix is an important element for numerical analysis, optimization and design of various electrical circuits. Cramer's rule is an explicit formula for the solution of a system of linear equations (SLE). For each variable, the denominator is the determinant of the matrix of coeffi ...
... The determinant of matrix is an important element for numerical analysis, optimization and design of various electrical circuits. Cramer's rule is an explicit formula for the solution of a system of linear equations (SLE). For each variable, the denominator is the determinant of the matrix of coeffi ...
Matrix completion

In mathematics, matrix completion is the process of adding entries to a matrix which has some unknown or missing values.In general, given no assumptions about the nature of the entries, matrix completion is theoretically impossible, because the missing entries could be anything. However, given a few assumptions about the nature of the matrix, various algorithms allow it to be reconstructed. Some of the most common assumptions made are that the matrix is low-rank, the observed entries are observed uniformly at random and the singular vectors are separated from the canonical vectors. A well known method for reconstructing low-rank matrices based on convex optimization of the nuclear norm was introduced by Emmanuel Candès and Benjamin Recht.