January 2016 - Stony Brook University
... b) (4 points) Describe the algorithm of Newton’s method for solving the nonlinear equation ∇L(x, y, λ) = 0 to obtain the critical points (x∗ , y∗ , λ∗ ). Show one step of the Newton’s method the initial guess (x0 = 1, y0 = 2, λ0 = 0). c) (3 points) Is (x∗ , y∗ , λ∗ ) a minimum, maximum, or saddle po ...
... b) (4 points) Describe the algorithm of Newton’s method for solving the nonlinear equation ∇L(x, y, λ) = 0 to obtain the critical points (x∗ , y∗ , λ∗ ). Show one step of the Newton’s method the initial guess (x0 = 1, y0 = 2, λ0 = 0). c) (3 points) Is (x∗ , y∗ , λ∗ ) a minimum, maximum, or saddle po ...
Here
... using a quadratic in x as the approximating function. b) Solve the problem by collocation, setting the residual to zero at x = 0.5. c) Solve the problem by Galerkin’s method. 5. Develop the elements equations for a 10-cm rod with boundary conditions of T(0, t) = 40 and T(10, t) = 100 and a uniform h ...
... using a quadratic in x as the approximating function. b) Solve the problem by collocation, setting the residual to zero at x = 0.5. c) Solve the problem by Galerkin’s method. 5. Develop the elements equations for a 10-cm rod with boundary conditions of T(0, t) = 40 and T(10, t) = 100 and a uniform h ...
§3.1 Introduction / Newton-Cotes / The Trapezium Rule
... Given a real-valued function f that is continuous on [a, b], can we find an estimate for Z b ...
... Given a real-valued function f that is continuous on [a, b], can we find an estimate for Z b ...
Statistical Computing and Simulation
... could count “nlminb” as one of the method (for replacing Newton’s method). Also, similar to what we saw in the class, discuss what is the influence of starting points to the number of iterations. Experiment with as many variance reduction techniques as you can think of to apply the problem of evalua ...
... could count “nlminb” as one of the method (for replacing Newton’s method). Also, similar to what we saw in the class, discuss what is the influence of starting points to the number of iterations. Experiment with as many variance reduction techniques as you can think of to apply the problem of evalua ...
method - csc113ksu
... The Method toString • Implementing toString method in java is done by overriding the Object’s toString method. • The java toString() method is used when we need a string representation of an object. • It is defined in Object class. • This method can be overridden to customize the String representat ...
... The Method toString • Implementing toString method in java is done by overriding the Object’s toString method. • The java toString() method is used when we need a string representation of an object. • It is defined in Object class. • This method can be overridden to customize the String representat ...
Computerised Mathematical Methods in Engineering
... This means that all ci,j are determined by values inside the boundaries Initial condition [e.g. c(x,0)=sin(xπ)] must satisfy boundary conditions [e.g. c(0,t)=0] ...
... This means that all ci,j are determined by values inside the boundaries Initial condition [e.g. c(x,0)=sin(xπ)] must satisfy boundary conditions [e.g. c(0,t)=0] ...
Practice Final
... 7. Find a, b, c such that y = a2 + b cos 2x + c sin 3x is the least square approximation to y = x in [−π, π] with respect to the weight function w(x) = 1. 8. Derive the nonlinear system for a, b such that the exponential function y = beax fit the following data points, (1.0, 1.0), (1.2, 1.4), (1.5, ...
... 7. Find a, b, c such that y = a2 + b cos 2x + c sin 3x is the least square approximation to y = x in [−π, π] with respect to the weight function w(x) = 1. 8. Derive the nonlinear system for a, b such that the exponential function y = beax fit the following data points, (1.0, 1.0), (1.2, 1.4), (1.5, ...
Chapter 4 part 2 Runge
... One problem with the Muskingum method is that it assumes that the storage equation is linear with depth. Although this simplifies calculation considerably, it doesn’t necessarily have anything to do with reality. A more accurate method would allow for the storage function to be any function of depth ...
... One problem with the Muskingum method is that it assumes that the storage equation is linear with depth. Although this simplifies calculation considerably, it doesn’t necessarily have anything to do with reality. A more accurate method would allow for the storage function to be any function of depth ...
A proposal of variant of BiCGSafe method based on optimized
... of combination of two polynomials was generalized as a form of product of two polynomials in 1997. However, the optimization of product of polynomials remains as an open problem. The first solution among neive realization of product-type iterative methods was made partly by Fujino et al. in 2005 owi ...
... of combination of two polynomials was generalized as a form of product of two polynomials in 1997. However, the optimization of product of polynomials remains as an open problem. The first solution among neive realization of product-type iterative methods was made partly by Fujino et al. in 2005 owi ...
3 Approximating a function by a Taylor series
... What does this mean for computation? In nearly all our computations, we will replace exact formulations with approximations. For example, we approximate continuous quantities with discrete quantities, we are limited in size by floating point representation of numbers which often necessitates roundin ...
... What does this mean for computation? In nearly all our computations, we will replace exact formulations with approximations. For example, we approximate continuous quantities with discrete quantities, we are limited in size by floating point representation of numbers which often necessitates roundin ...
The calculation of the degree of an approximate greatest common
... The calculation of the degree of an approximate greatest common divisor (AGCD) of two inexact polynomials f (y) and g(y) is a non-trivial computation because it reduces to the estimation of the rank loss of a resultant matrix R(f, g). This computation is usually performed by placing a threshold on t ...
... The calculation of the degree of an approximate greatest common divisor (AGCD) of two inexact polynomials f (y) and g(y) is a non-trivial computation because it reduces to the estimation of the rank loss of a resultant matrix R(f, g). This computation is usually performed by placing a threshold on t ...
Integration Formulas
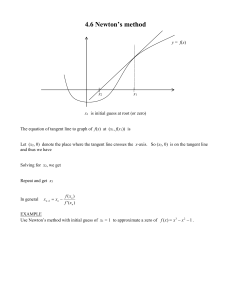
... Use Newton’s method with initial guess of x1 = 1 to approximate a zero of f (x) x 3 x 2 1 . ...
... Use Newton’s method with initial guess of x1 = 1 to approximate a zero of f (x) x 3 x 2 1 . ...
BBA IInd SEMESTER EXAMINATION 2008-09
... Note: Attempt six questions in all. Q. No. 1 is compulsory. ...
... Note: Attempt six questions in all. Q. No. 1 is compulsory. ...