Use of Genetic Algorithms for Finding Roots of Algebraic Equations
... Algorithms for solving root problems numerically can be divided into two main groups: direct methods and iterative methods. Direct methods are those which can be completed in a predetermined finite number of steps. Iterative methods are methods which converge to the solution over time. An iteration ...
... Algorithms for solving root problems numerically can be divided into two main groups: direct methods and iterative methods. Direct methods are those which can be completed in a predetermined finite number of steps. Iterative methods are methods which converge to the solution over time. An iteration ...
Finding the Greatest Common Divisor by repeated
... The method thus works because of the principle, which results from the above theorems and corollary, that the GCD of two numbers remains unchanged when the larger number is replaced by its difference with the smaller number. EXTENSION Although the general proof gets a little technical, it is worth n ...
... The method thus works because of the principle, which results from the above theorems and corollary, that the GCD of two numbers remains unchanged when the larger number is replaced by its difference with the smaller number. EXTENSION Although the general proof gets a little technical, it is worth n ...
Advanced Numerical Methods - Université catholique de Louvain
... -To select and to apply the right method for a given problem. -To evaluate the algorithmic complexity of a method. -To efficiently use the numerical available libraries (Lapack) -To provide an estimate of the error. -To evaluate the quality of a mesh for a given method. -To perform a calculation on ...
... -To select and to apply the right method for a given problem. -To evaluate the algorithmic complexity of a method. -To efficiently use the numerical available libraries (Lapack) -To provide an estimate of the error. -To evaluate the quality of a mesh for a given method. -To perform a calculation on ...
Style E 24 by 48
... By approximating the Radon transform with a Fejér series instead, we obtain the Fejér-mFBP algorithm: ...
... By approximating the Radon transform with a Fejér series instead, we obtain the Fejér-mFBP algorithm: ...
Runge-Kutta Methods
... does not meet the user prescribed tolerance If this is the case, the step size should be decrased, yn is rejected and it’s to be computed again… ...
... does not meet the user prescribed tolerance If this is the case, the step size should be decrased, yn is rejected and it’s to be computed again… ...
X - EGR 115!
... Numerical methods are techniques used to find quantitative solutions to mathematical problems. Many numerical methods are iterative solutions – this means that the technique is applied over and over, gradually getting closer (i.e. converging) on the final answer. Iterative solutions are complete whe ...
... Numerical methods are techniques used to find quantitative solutions to mathematical problems. Many numerical methods are iterative solutions – this means that the technique is applied over and over, gradually getting closer (i.e. converging) on the final answer. Iterative solutions are complete whe ...
Solution of manning equation by Newton Raphson Method
... Solution of manning equation by Newton Raphson Method There is no general analytical solution to manning equation for determining the flow depth given the flow rate because the area A and hydraulic radius R may be complicated functions of the depth. Newton Raphson method can be applied iteratively t ...
... Solution of manning equation by Newton Raphson Method There is no general analytical solution to manning equation for determining the flow depth given the flow rate because the area A and hydraulic radius R may be complicated functions of the depth. Newton Raphson method can be applied iteratively t ...
Invoking methods in the Java library
... method in the Java standard library. • The cosine function is implemented as the Math.cos method in the Java standard library. • The square root function is implemented as the Math.sqrt method in the Java standard library. ...
... method in the Java standard library. • The cosine function is implemented as the Math.cos method in the Java standard library. • The square root function is implemented as the Math.sqrt method in the Java standard library. ...
Solving a Cubic Equation by Perturbation Theory
... You probably do not know how to solve the equation x3 + ...
... You probably do not know how to solve the equation x3 + ...
Java Programming class – Department of Network
... programming language. If a class is declared with no extends clause, then the compiler adds implicitly the code extend Object to the declaration for example Public class Employee { // code here ...
... programming language. If a class is declared with no extends clause, then the compiler adds implicitly the code extend Object to the declaration for example Public class Employee { // code here ...
How do you compute the inverse of the Prandtl
... All of the constants shown here are for γ=7/5. The original paper by Hall describes the calculation for other specific heats. The accuracy of the Hall approximation is quite good with the maximum error much less that one-tenth of one percent. ...
... All of the constants shown here are for γ=7/5. The original paper by Hall describes the calculation for other specific heats. The accuracy of the Hall approximation is quite good with the maximum error much less that one-tenth of one percent. ...
DOCX
... Question 7: master method example T(n) = 3T(n/2) + nlogn Use the Master-Method to find T(n). Solution: a = 3, b = 2, f(n) = nlogn We assume it's the 1-st case of a Master Theorem, so we need to show that: nlogn = O(nlog23 - ε) x= log 2 3 1.585 nlogn ≤ cn x logn ≤ cn x 1 We may operate log on ...
... Question 7: master method example T(n) = 3T(n/2) + nlogn Use the Master-Method to find T(n). Solution: a = 3, b = 2, f(n) = nlogn We assume it's the 1-st case of a Master Theorem, so we need to show that: nlogn = O(nlog23 - ε) x= log 2 3 1.585 nlogn ≤ cn x logn ≤ cn x 1 We may operate log on ...
Analytic calculation of the nonzero fast wave reflection coefficient
... that all coefficients r; can be calculated exactly by some algebraic recurrence formula, although they are in general rather lengthy to be written out explicitly. This series is useful only if it is convergent, unless we know how to sum it analytically. However, due to the complicated nature of the ...
... that all coefficients r; can be calculated exactly by some algebraic recurrence formula, although they are in general rather lengthy to be written out explicitly. This series is useful only if it is convergent, unless we know how to sum it analytically. However, due to the complicated nature of the ...
Solving Two-Point Second Order Boundary Value Problems Using
... second order boundary value problem using collocation method with Haar wavelets while Liang and Jeffrey (2010) adopted the homotopy analysis method to solve the two point second order boundary value problem. Hasni, Majid and Senu (2013), Jator and Li (2009), Sagir (2013) and See, Majid and Suleiman ...
... second order boundary value problem using collocation method with Haar wavelets while Liang and Jeffrey (2010) adopted the homotopy analysis method to solve the two point second order boundary value problem. Hasni, Majid and Senu (2013), Jator and Li (2009), Sagir (2013) and See, Majid and Suleiman ...
Footnotes to the flowchart
... 13. Has the laboratory reported the correct method and result? NO (I): The internal routines have to be reevaluated. 14. Have the samples been sent in a proper way? NO (E): If the other results imply poor material, contact the actual EQA-organizer to check if there might have been any problem with t ...
... 13. Has the laboratory reported the correct method and result? NO (I): The internal routines have to be reevaluated. 14. Have the samples been sent in a proper way? NO (E): If the other results imply poor material, contact the actual EQA-organizer to check if there might have been any problem with t ...
Quasi.py - U.I.U.C. Math
... unit distances away from the origin At points where three planes intersect, transport corresponding vectors and perform the vector addition, drawing a rhombohedron, either fat or skinny Drawing enough rhombohedra reveals a quasiperiodic pattern This is the method I employed in my program ...
... unit distances away from the origin At points where three planes intersect, transport corresponding vectors and perform the vector addition, drawing a rhombohedron, either fat or skinny Drawing enough rhombohedra reveals a quasiperiodic pattern This is the method I employed in my program ...
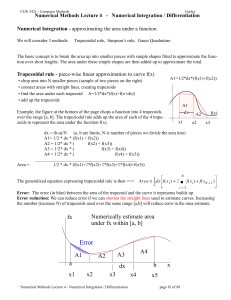
NM_lect_4 - essie-uf
... • Also, the derivation provides that the answer is exact if the function being integrated is a polynomial up to third order!! The extension: What if the range of integration is not [ -1 , 1 ] ?? Let’s say & # & when the range is [ -1 , 1 ]. Let’s also say the range of interest is [ a , b ] Skipping ...
... • Also, the derivation provides that the answer is exact if the function being integrated is a polynomial up to third order!! The extension: What if the range of integration is not [ -1 , 1 ] ?? Let’s say & # & when the range is [ -1 , 1 ]. Let’s also say the range of interest is [ a , b ] Skipping ...
Math Help Algebra
... Completing the square is a method used to solve quadratic equations. Algebraic properties are used to manipulate the quadratic polynomial to change its form. This method is one way to derive the quadratic formula. ...
... Completing the square is a method used to solve quadratic equations. Algebraic properties are used to manipulate the quadratic polynomial to change its form. This method is one way to derive the quadratic formula. ...
Lecture: 9
... as e-t while the other decays as e-tb, which will be much faster if b is large. A nonhomogeneous linear system x’(t) = Ax +f(t) could stiff either because the eigenvalues of A differ considerably from each other or because the transient solution decays on a time scale very different from that approp ...
... as e-t while the other decays as e-tb, which will be much faster if b is large. A nonhomogeneous linear system x’(t) = Ax +f(t) could stiff either because the eigenvalues of A differ considerably from each other or because the transient solution decays on a time scale very different from that approp ...
1 Time-Integrators
... k represents the order of accuracy of the numerical scheme (e.g., RungeKutta) used to solve this equation while N represents the order of interpolation used to compute the variables at the departure points • Therefore, if we use either high order k with low order N or vice-versa, then we limit the o ...
... k represents the order of accuracy of the numerical scheme (e.g., RungeKutta) used to solve this equation while N represents the order of interpolation used to compute the variables at the departure points • Therefore, if we use either high order k with low order N or vice-versa, then we limit the o ...
4yx = + 2 xy = ⌋ ⌉ ⌊ ⌈ = xy 11 J ⌋ ⌉ ⌊ ⌈ -
... The standard normal distribution value was obtained from appendix A.3 of WMM. (b) What PDF did you use to solve part (a)? I would use the normal distribution because the molecular weight can be considered to be a continuous variable. Moreover, we only know the mean and the variance, so we have enoug ...
... The standard normal distribution value was obtained from appendix A.3 of WMM. (b) What PDF did you use to solve part (a)? I would use the normal distribution because the molecular weight can be considered to be a continuous variable. Moreover, we only know the mean and the variance, so we have enoug ...
Finite Difference Methods in 2d Heat Transfer
... It is also possible to simulate materials with variable heat diffusivity to simulate conduction in e.g. “layered” materials. The “heart” of this 2d code is the computation of dT in the .m file computedT.m dT=dt*DivDiv(T,nu,east,west,north,south,inx,iny,dx,dy); - In short the “cryptic” function DivDi ...
... It is also possible to simulate materials with variable heat diffusivity to simulate conduction in e.g. “layered” materials. The “heart” of this 2d code is the computation of dT in the .m file computedT.m dT=dt*DivDiv(T,nu,east,west,north,south,inx,iny,dx,dy); - In short the “cryptic” function DivDi ...
Modification of the HPM by using optimal Newton
... F. Ghomanjani, F. Divandar/ J. Math. Computer Sci. 14 (2015), 162-170 ...
... F. Ghomanjani, F. Divandar/ J. Math. Computer Sci. 14 (2015), 162-170 ...