Numerical Study on ESR of Nanomagnet V and Dzyaloshinsky-Moriya In- teraction
... We develop an efficient numerical method to obtain the ESR absorption of nanoscale molecular magnets. Our new method realizes O(N ) calculation both in computer memory and computation time. The method avoids direct diagonalization with the help of the random vector technique and the Chebyshev polyno ...
... We develop an efficient numerical method to obtain the ESR absorption of nanoscale molecular magnets. Our new method realizes O(N ) calculation both in computer memory and computation time. The method avoids direct diagonalization with the help of the random vector technique and the Chebyshev polyno ...
Methods: Documentation, Reference Parameters, Command
... Find the area of a triangle given the lengths of the sides. Find the area of a rectangle given the length and width. Find the area of a regular pentagon given the length of a side. o Depending on the input, take in the appropriate input in order to perform the function (coordinates, lengths of s ...
... Find the area of a triangle given the lengths of the sides. Find the area of a rectangle given the length and width. Find the area of a regular pentagon given the length of a side. o Depending on the input, take in the appropriate input in order to perform the function (coordinates, lengths of s ...
Convergence of Newton-like methods for solving systems of
... of nonlinear equations. However, this notion m a y be extremely useful for testing programs implementing Newton-like methods. Test functions can be created such t h a t all information required for calculating the solvability n u m b e r is available. We can therefore create a representative set of ...
... of nonlinear equations. However, this notion m a y be extremely useful for testing programs implementing Newton-like methods. Test functions can be created such t h a t all information required for calculating the solvability n u m b e r is available. We can therefore create a representative set of ...
NARESUAN UNIVERSITY FACULTY OF ENGINEERING The Finite
... transfer, fluid flow, magnetic field, soil-structure interaction, and fluid-structuresoil interaction problems. Finding a solution that satisfies a differential equation throughout a domain (or region) as well as the boundary conditions is very difficult (if not impossible) for all but the most elem ...
... transfer, fluid flow, magnetic field, soil-structure interaction, and fluid-structuresoil interaction problems. Finding a solution that satisfies a differential equation throughout a domain (or region) as well as the boundary conditions is very difficult (if not impossible) for all but the most elem ...
3.1/3.2 Solving Systems of Equations by Substitution Method
... 1. Draw line under original problem ...
... 1. Draw line under original problem ...
EIGENVECTOR CALCULATION Let A have an approximate
... λI is almost singular. How do we find a corresponding eigenvector? If the eigenvalue is of multiplicity 1, then in linear algebra courses we usually just try to solve the linear system (A − λI ) x = 0 Oversimplifying, we usually drop one of the equations, arbitrarily assign one of the components of ...
... λI is almost singular. How do we find a corresponding eigenvector? If the eigenvalue is of multiplicity 1, then in linear algebra courses we usually just try to solve the linear system (A − λI ) x = 0 Oversimplifying, we usually drop one of the equations, arbitrarily assign one of the components of ...
Unlicensed-7-PDF801-804_engineering optimization
... works well for a given class of problems may work poorly for others. Hence it is usually necessary to try more than one method to solve a particular problem efficiently. Further, the efficiency of any nonlinear programming method depends largely on the values of adjustable parameters such as startin ...
... works well for a given class of problems may work poorly for others. Hence it is usually necessary to try more than one method to solve a particular problem efficiently. Further, the efficiency of any nonlinear programming method depends largely on the values of adjustable parameters such as startin ...
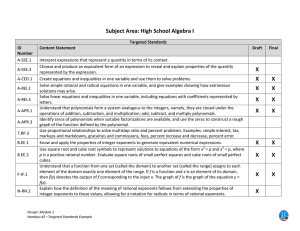
Document
... Know and apply the properties of integer exponents to generate equivalent numerical expressions. Use square root and cube root symbols to represent solutions to equations of the form x2 = p and x3 = p, where p is a positive rational number. Evaluate square roots of small perfect squares and cube roo ...
... Know and apply the properties of integer exponents to generate equivalent numerical expressions. Use square root and cube root symbols to represent solutions to equations of the form x2 = p and x3 = p, where p is a positive rational number. Evaluate square roots of small perfect squares and cube roo ...
Full text
... {Fp +1/FF }. These results generalize to quadratic equations with roots of unequal magnitudes, It is well known that the ratios of successive Fibonacci numbers converge to the golden mean. We recall that the Fibonacci numbers {Fn} are defined by the recurrence Fn = Fn_1 + Fn_2 with F 0 = 0 and F1 =. ...
... {Fp +1/FF }. These results generalize to quadratic equations with roots of unequal magnitudes, It is well known that the ratios of successive Fibonacci numbers converge to the golden mean. We recall that the Fibonacci numbers {Fn} are defined by the recurrence Fn = Fn_1 + Fn_2 with F 0 = 0 and F1 =. ...
Methods
... When a method is called, the statements inside the corresponding method are executed When all statements in the method has been executed, the execution will resume at the program location of the method call ...
... When a method is called, the statements inside the corresponding method are executed When all statements in the method has been executed, the execution will resume at the program location of the method call ...
Introduction to Integration
... Write a program to find the value of the following function using trapezoidal method, take n=60 ...
... Write a program to find the value of the following function using trapezoidal method, take n=60 ...
A new approach to analysis of free beam vibrations
... The initial-boundary problem for the linear theory of elasticity is considered. Based on the method of integrodifferential relations a new dynamical variational principle in which displacement, stress, and momentum functions are varied is proposed and discussed [1–5]. To minimize the nonnegative fun ...
... The initial-boundary problem for the linear theory of elasticity is considered. Based on the method of integrodifferential relations a new dynamical variational principle in which displacement, stress, and momentum functions are varied is proposed and discussed [1–5]. To minimize the nonnegative fun ...
Divide unit missing in a supercomputer?
... This one is the acceptable iterative formula to find the inverse of a as it does not involve division. Starting with an initial guess for the inverse of a , one can find newer approximations by using the above iterative formula. Each iteration requires two multiplications and one subtraction. Howeve ...
... This one is the acceptable iterative formula to find the inverse of a as it does not involve division. Starting with an initial guess for the inverse of a , one can find newer approximations by using the above iterative formula. Each iteration requires two multiplications and one subtraction. Howeve ...
DOC
... This one is the acceptable iterative formula to find the inverse of a as it does not involve division. Starting with an initial guess for the inverse of a , one can find newer approximations by using the above iterative formula. Each iteration requires two multiplications and one subtraction. Howeve ...
... This one is the acceptable iterative formula to find the inverse of a as it does not involve division. Starting with an initial guess for the inverse of a , one can find newer approximations by using the above iterative formula. Each iteration requires two multiplications and one subtraction. Howeve ...
Nonlinear Root Finding and a Glimpse at Optimization
... The simplest root-finding method is the bisection method, which basically just performs a simple binary search. We begin by bracketing the root: this means finding two points x1 and x2 at which f (x) has different signs, so that we are guaranteed2 to have a root between x1 and x2 . Then we bisect th ...
... The simplest root-finding method is the bisection method, which basically just performs a simple binary search. We begin by bracketing the root: this means finding two points x1 and x2 at which f (x) has different signs, so that we are guaranteed2 to have a root between x1 and x2 . Then we bisect th ...
Latent Friend Mining..
... as well as much interesting information on the blogs. Take MSN spaces as an example, the bloggers may put their favorite songs, sports, pictures on the blogs. ...
... as well as much interesting information on the blogs. Take MSN spaces as an example, the bloggers may put their favorite songs, sports, pictures on the blogs. ...
public static void nameAndAddress()
... Methods that Use a Single Argument • Methods that do not require any arguments are simple to write and can be used in certain situations. • However, they are limited because they have no communication with the calling class. Ex. Suppose you are writing a program to create restaurant reservations. W ...
... Methods that Use a Single Argument • Methods that do not require any arguments are simple to write and can be used in certain situations. • However, they are limited because they have no communication with the calling class. Ex. Suppose you are writing a program to create restaurant reservations. W ...
Advanced Object Oriented Systems
... accessible and there is no other applicable and accessible method that is more specific. • If there is only one maximally specific method for a given method invocation, it is called the most specific method • If a most specific method cannot be found, there is ambiguity and the compiler reports an e ...
... accessible and there is no other applicable and accessible method that is more specific. • If there is only one maximally specific method for a given method invocation, it is called the most specific method • If a most specific method cannot be found, there is ambiguity and the compiler reports an e ...
Chapter 12: Copying with the Limitations of Algorithm Power
... decreasing order (i.e., from the largest to the smallest). Then proceed as above by placing an item in the first bin in which it fits and starting a new bin if there are no such bins Example: n = 4, s1 = 0.4, s2 = 0.2, s3 = 0.6, s4 = 0.7 ...
... decreasing order (i.e., from the largest to the smallest). Then proceed as above by placing an item in the first bin in which it fits and starting a new bin if there are no such bins Example: n = 4, s1 = 0.4, s2 = 0.2, s3 = 0.6, s4 = 0.7 ...
5th Grade Unit 2
... 4 in the thousands place, 7 in the ten-thousands place, 5 in the tenths place, and 8 in all of the remaining places. ____ ____ , ____ ____ ____ . ____ 14. Jack’s great-grandmother was born in 1910. His family had a big party for her birthday in 1996. There were 45 family members at the party. How ol ...
... 4 in the thousands place, 7 in the ten-thousands place, 5 in the tenths place, and 8 in all of the remaining places. ____ ____ , ____ ____ ____ . ____ 14. Jack’s great-grandmother was born in 1910. His family had a big party for her birthday in 1996. There were 45 family members at the party. How ol ...
exam_3_soluiton
... Where it is appropriate, write your answers on the screen-shot. Feel free to change the units if needed, or to fill in a value that you think will show up after your initial selection. ...
... Where it is appropriate, write your answers on the screen-shot. Feel free to change the units if needed, or to fill in a value that you think will show up after your initial selection. ...
Quiz #1
... The values of f(x) at 5 different points are plotted in the above graph. The horizontal line in the graph represents the x-axis. (a) Suppose the False-Position method is used to approximate the zero of f(x), and x1 and x5 are selected as the two initial points. Show the location of the estimated roo ...
... The values of f(x) at 5 different points are plotted in the above graph. The horizontal line in the graph represents the x-axis. (a) Suppose the False-Position method is used to approximate the zero of f(x), and x1 and x5 are selected as the two initial points. Show the location of the estimated roo ...
VARIOUS ESTIMATIONS OF π AS
... as values for certain variables in algorithms to generate random variates of chosen probability functions to be used in simulations of statistical models or to generate pseudo-random numbers for more complex probability functions . In this paper we will demonstrate a unique use of the Monte Carlo me ...
... as values for certain variables in algorithms to generate random variates of chosen probability functions to be used in simulations of statistical models or to generate pseudo-random numbers for more complex probability functions . In this paper we will demonstrate a unique use of the Monte Carlo me ...