Section 2.2 - Basic Differentiation Rules and Rates of Change
... Position Function The function s that gives the position (relative to the origin) of an object as a function of time t. Our functions will describe the motion of an object moving in a horizontal or vertical line. s(t) ...
... Position Function The function s that gives the position (relative to the origin) of an object as a function of time t. Our functions will describe the motion of an object moving in a horizontal or vertical line. s(t) ...
Lecture 3. Differentiation of functionals
... stationary condition and gradient method for its minimization if we had some methods of differentiation of this functional. Let us try to use the standard technique for calculate its derivative at a point v of the set V. It is know that the derivative of a function at a point is the result of passin ...
... stationary condition and gradient method for its minimization if we had some methods of differentiation of this functional. Let us try to use the standard technique for calculate its derivative at a point v of the set V. It is know that the derivative of a function at a point is the result of passin ...
HERE
... function is the slope of its graph, and so it must be negative when x is very small and positive when x is large (or vice-versa if the first term of the polynomial is negative). This means that the derivative of an even polynomial function cannot be even. A similar argument shows that the derivative ...
... function is the slope of its graph, and so it must be negative when x is very small and positive when x is large (or vice-versa if the first term of the polynomial is negative). This means that the derivative of an even polynomial function cannot be even. A similar argument shows that the derivative ...
Appendix B Lie groups and Lie algebras
... i.e. AJ0 = J0 A. We therefore can give an alternative definition of Cn×n : in addition to being the complex n2 -dimensional vector space of n-byn matrices, it is also the real 2n2 -dimensional vector space of matrices A ∈ R2n×2n such that AJ0 = J0 A. As such it is a linear subspace of R2n×2n , and w ...
... i.e. AJ0 = J0 A. We therefore can give an alternative definition of Cn×n : in addition to being the complex n2 -dimensional vector space of n-byn matrices, it is also the real 2n2 -dimensional vector space of matrices A ∈ R2n×2n such that AJ0 = J0 A. As such it is a linear subspace of R2n×2n , and w ...
Week 9: Differentiation Rules. - MA161/MA1161: Semester 1 Calculus.
... The derivative of a function f at a point p is the instantaneous rate of change of f at p. Derivatives can be computed from first principles, that is directly from the above definition. Differentiation rules are formulas which simplify differentiation tasks, and apply to wide ranges of functions. ...
... The derivative of a function f at a point p is the instantaneous rate of change of f at p. Derivatives can be computed from first principles, that is directly from the above definition. Differentiation rules are formulas which simplify differentiation tasks, and apply to wide ranges of functions. ...
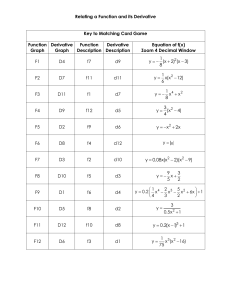
description of derivative
... The graph of this derivative is not positive for all x in [–3, 3], and is symmetric to the y-axis. d1 ...
... The graph of this derivative is not positive for all x in [–3, 3], and is symmetric to the y-axis. d1 ...
The Tangent Line Problem
... The Tangent Line Problem Essentially, the problem of finding the tangent line at a point P boils down to the problem of finding the slope of the tangent line at point P. You can approximate this slope using a secant line through the point of tangency and a second point on the ...
... The Tangent Line Problem Essentially, the problem of finding the tangent line at a point P boils down to the problem of finding the slope of the tangent line at point P. You can approximate this slope using a secant line through the point of tangency and a second point on the ...
Chapter 4 Theory - AlexanderAcademics.com
... Sec. 3.1 Extrema on an Interval Theorem: The Extreme Value Theorem If f is continuous on [a, b] then f has both an absolute maximum and minimum on [a, b]. This just says that if a function is continuous in going from the point (a, f(a)) to (b, f(b)), then somewhere in the interval is a highest point ...
... Sec. 3.1 Extrema on an Interval Theorem: The Extreme Value Theorem If f is continuous on [a, b] then f has both an absolute maximum and minimum on [a, b]. This just says that if a function is continuous in going from the point (a, f(a)) to (b, f(b)), then somewhere in the interval is a highest point ...
Solution - Math TAMU
... asymptotes when x = ±1, and the x-axis is a horizontal asymptote when x → ±∞. In order for the graph to have negative slope everywhere on its domain and to have the origin as its only inflection point, the graph must look something like the following figure. ...
... asymptotes when x = ±1, and the x-axis is a horizontal asymptote when x → ±∞. In order for the graph to have negative slope everywhere on its domain and to have the origin as its only inflection point, the graph must look something like the following figure. ...
Derivatives - Pauls Online Math Notes
... Sketch picture and identify known/unknown quantities. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. add on a derivative every time you differentiate a function of t). Plug in known quantities and solve for the unknown quantity. Ex. A ...
... Sketch picture and identify known/unknown quantities. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. add on a derivative every time you differentiate a function of t). Plug in known quantities and solve for the unknown quantity. Ex. A ...
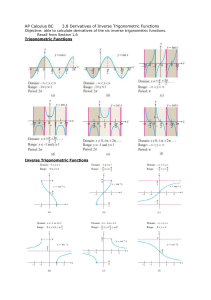
3.8 Derivatives of Inverse Trig Functions
... is never zero on I , then f has an inverse and f −1 at every point on the interval f ( I ) . ...
... is never zero on I , then f has an inverse and f −1 at every point on the interval f ( I ) . ...
AP Calculus AB
... Justifications for vertical tangent lines: dy f ( x ) has vertical tangents when is undefined. dx Justifications for Particle Motion: Particle is moving right/up because v(t ) 0 (positive). Particle is moving left/down because v(t ) 0 (negative). ...
... Justifications for vertical tangent lines: dy f ( x ) has vertical tangents when is undefined. dx Justifications for Particle Motion: Particle is moving right/up because v(t ) 0 (positive). Particle is moving left/down because v(t ) 0 (negative). ...
x - baiermathstudies
... Values of x where f ′(x) is given. Equation of the tangent at a given point. Increasing and decreasing functions. Graphical interpretation of f′(x)>0, f′(x)=0, f′(x)<0. Values of x where the gradient of a curve is 0 (zero): solution of f′(x) =0. • Local maximum and minimum points. ...
... Values of x where f ′(x) is given. Equation of the tangent at a given point. Increasing and decreasing functions. Graphical interpretation of f′(x)>0, f′(x)=0, f′(x)<0. Values of x where the gradient of a curve is 0 (zero): solution of f′(x) =0. • Local maximum and minimum points. ...
Solution - Cornell Math
... (e) Let f be as in part (d). Find a point x such that the tangent line to f is horizontal. Solution 3.2. (a) The tangent line to the graph of a function f at the point a is the line that is “closest” to the graph of f at a. It is the line that best approximates f at that point. It can give an idea o ...
... (e) Let f be as in part (d). Find a point x such that the tangent line to f is horizontal. Solution 3.2. (a) The tangent line to the graph of a function f at the point a is the line that is “closest” to the graph of f at a. It is the line that best approximates f at that point. It can give an idea o ...
Homework 4
... • V (t) = i (ai sinh(t −K) + bi cosh(t −K))ei (t) if K < 0 for suitable constants ai , bi . Problem 2. If we think of S 3 as the unit sphere in C2 (with its standard Hermitian metric), multiplication of the coordinates by eiθ exhibits S 3 as a principal S 1 bundle over S 2 (this is usually known as ...
... • V (t) = i (ai sinh(t −K) + bi cosh(t −K))ei (t) if K < 0 for suitable constants ai , bi . Problem 2. If we think of S 3 as the unit sphere in C2 (with its standard Hermitian metric), multiplication of the coordinates by eiθ exhibits S 3 as a principal S 1 bundle over S 2 (this is usually known as ...
12. Vectors and the geometry of space 12.1. Three dimensional
... 12. Vectors and the geometry of space 12.1. Three dimensional coordinate systems. To locate a point in space, one needs to choose a point first as the reference, which is usually called the origin. Then, select three directed lines and labelled the x-axis, y-axis and z-axis. These three lines are nam ...
... 12. Vectors and the geometry of space 12.1. Three dimensional coordinate systems. To locate a point in space, one needs to choose a point first as the reference, which is usually called the origin. Then, select three directed lines and labelled the x-axis, y-axis and z-axis. These three lines are nam ...
Here
... (iv) A manufacturer models their costs using the function c(q) = 41 q 2 −2q+ q. What is their average cost when q = 5? What is their marginal cost when q = 5? (d) 11.4 Product rule and quotient rule. (i) f (4) = 2, f 0 (4) = 5, g(4) = −1 and g 0 (4) = 12 . What are (f g)0 (4) and (f /g)0 (4)? (ii) F ...
... (iv) A manufacturer models their costs using the function c(q) = 41 q 2 −2q+ q. What is their average cost when q = 5? What is their marginal cost when q = 5? (d) 11.4 Product rule and quotient rule. (i) f (4) = 2, f 0 (4) = 5, g(4) = −1 and g 0 (4) = 12 . What are (f g)0 (4) and (f /g)0 (4)? (ii) F ...
Divergence and Curl of a Vector Field
... derivative in one of the variables is given, as seen earlier. However, when several partial derivatives of an unknown function are given simultaneously, there may not be any function with those values! In particular, the gradient field for smooth functions must respect Clairaut’s theorem, so not eve ...
... derivative in one of the variables is given, as seen earlier. However, when several partial derivatives of an unknown function are given simultaneously, there may not be any function with those values! In particular, the gradient field for smooth functions must respect Clairaut’s theorem, so not eve ...
a review sheet for test #02
... The derivative of the function f(x) is defined as f x h f x f ' x lim ...
... The derivative of the function f(x) is defined as f x h f x f ' x lim ...
Chapter 03 - Mathematical Marketing
... variables, f (x) / x . Note that the function of the vector, f(x'), is a scalar. To begin, we will start with the constant function, that is, f(x') = c where c is a constant (scalar). The derivative of this function with respect to the row vector x' is itself a row vector with the same order as ...
... variables, f (x) / x . Note that the function of the vector, f(x'), is a scalar. To begin, we will start with the constant function, that is, f(x') = c where c is a constant (scalar). The derivative of this function with respect to the row vector x' is itself a row vector with the same order as ...
LECTURE 30: INDUCED MAPS BETWEEN CLASSIFYING SPACES
... α∗ : {Gbundles over X} → {Hbundles over X}. Namely, send a Gbundle E → X to the Hbundle H ×G E → X where G acts on H through the homomorphism α. Thus B may be viewed as a functor Topological groups → homotopy category of CWcomplexes. There is one particular case where the induced map admits a m ...
... α∗ : {Gbundles over X} → {Hbundles over X}. Namely, send a Gbundle E → X to the Hbundle H ×G E → X where G acts on H through the homomorphism α. Thus B may be viewed as a functor Topological groups → homotopy category of CWcomplexes. There is one particular case where the induced map admits a m ...