Universal cover of a Lie group. Last time Andrew Marshall
... 4) Suppose that G acts on a manifold M and that E → M is a fiber bundle over M . The action of G may not lift to an action on E. But the action of G̃ via π : G̃ → G does extend to an action on E¿ 5) If G is compact, connected with finite fundamental group then there are a finite number of compact co ...
... 4) Suppose that G acts on a manifold M and that E → M is a fiber bundle over M . The action of G may not lift to an action on E. But the action of G̃ via π : G̃ → G does extend to an action on E¿ 5) If G is compact, connected with finite fundamental group then there are a finite number of compact co ...
1300Y Geometry and Topology, Assignment 1 Exercise 1. Let Γ be a
... Exercise 1. Let Γ be a discrete group (a group with a countable number of elements, each one of which is an open set). Show (easy) that Γ is a zerodimensional Lie group. Suppose that Γ acts smoothly on a manifold M̃ , meaning that the action map θ :Γ × M̃ −→ M̃ (h, x) 7→ h · x is C ∞ . Suppose also ...
... Exercise 1. Let Γ be a discrete group (a group with a countable number of elements, each one of which is an open set). Show (easy) that Γ is a zerodimensional Lie group. Suppose that Γ acts smoothly on a manifold M̃ , meaning that the action map θ :Γ × M̃ −→ M̃ (h, x) 7→ h · x is C ∞ . Suppose also ...
PDF
... An ordered vector space whose underlying poset is a lattice is called a vector lattice. A vector lattice is also called a Riesz space. For example, given a topological space X, its ring of continuous functions C(X) is a vector lattice. In particular, any finite dimensional Euclidean space Rn is a ve ...
... An ordered vector space whose underlying poset is a lattice is called a vector lattice. A vector lattice is also called a Riesz space. For example, given a topological space X, its ring of continuous functions C(X) is a vector lattice. In particular, any finite dimensional Euclidean space Rn is a ve ...
Differential geometry of surfaces in Euclidean space
... Consequently, the associated Christoffel symbol is symmetric under the exchange of its lower indices. This encodes the intuitively clear fact that if we shift two coordinates, y µ and y ν , by unity, the result does not depend on the order of these two operations. Using this symmetry and the definit ...
... Consequently, the associated Christoffel symbol is symmetric under the exchange of its lower indices. This encodes the intuitively clear fact that if we shift two coordinates, y µ and y ν , by unity, the result does not depend on the order of these two operations. Using this symmetry and the definit ...
Practical Guide to Derivation
... In this example, a right triangle is used to estimate the slope between two points of a function, f(x). 'a' is a given value on the x-axis and 'h' is the change in the x axis from two points. Thus, we have one point, 'a', and another point, a+h. So, a < ∆x < a+h. The top point of the triangle is f(a ...
... In this example, a right triangle is used to estimate the slope between two points of a function, f(x). 'a' is a given value on the x-axis and 'h' is the change in the x axis from two points. Thus, we have one point, 'a', and another point, a+h. So, a < ∆x < a+h. The top point of the triangle is f(a ...
3.1 Properties of vector fields
... such that R × {x} ∩ U is connected, ϕ0 (x) = x for all x and if (t, x), (t + t0 , x), (t0 , ϕt (x)) are all in U then ϕt0 (ϕt (x)) = ϕt+t0 (x). Then the local existence and uniqueness of solutions to systems of ODE implies that every smooth vector field X ∈ Γ∞ (M, T M ) gives rise to a local 1-param ...
... such that R × {x} ∩ U is connected, ϕ0 (x) = x for all x and if (t, x), (t + t0 , x), (t0 , ϕt (x)) are all in U then ϕt0 (ϕt (x)) = ϕt+t0 (x). Then the local existence and uniqueness of solutions to systems of ODE implies that every smooth vector field X ∈ Γ∞ (M, T M ) gives rise to a local 1-param ...
Properties of the Derivative — Lecture 9. Recall that the average
... More generally, given a function y = f (x), the derivative of f is the function y = f 0(x) whose domain is the set of all x at which f 0(x) exists and is then given by the rule f 0(x) = the derivative of f at the point x. For many functions f we can with relative ease can calculate approximately th ...
... More generally, given a function y = f (x), the derivative of f is the function y = f 0(x) whose domain is the set of all x at which f 0(x) exists and is then given by the rule f 0(x) = the derivative of f at the point x. For many functions f we can with relative ease can calculate approximately th ...
vector
... 9.4 Vectors in the Plane magnitude of v: denoted |v|, it is the length of the vector. direction of v: the direction in which the arrow points initial point: the starting point of the arrow, also called the “tail” terminal point: the ending point of the arrow, also called the “head” ...
... 9.4 Vectors in the Plane magnitude of v: denoted |v|, it is the length of the vector. direction of v: the direction in which the arrow points initial point: the starting point of the arrow, also called the “tail” terminal point: the ending point of the arrow, also called the “head” ...
PDF
... A topological vector space is a pair (V, T ), where V is a vector space over a topological field K, and T is a topology on V such that under T the scalar multiplication (λ, v) 7→ λv is a continuous function K × V → V and the vector addition (v, w) 7→ v + w is a continuous function V × V → V , where ...
... A topological vector space is a pair (V, T ), where V is a vector space over a topological field K, and T is a topology on V such that under T the scalar multiplication (λ, v) 7→ λv is a continuous function K × V → V and the vector addition (v, w) 7→ v + w is a continuous function V × V → V , where ...
Problem Set 1
... (3) Let f : S 1 → R3 be a continuous, injective map. Prove that the image f (S 1 ) of f is homeomorphic to S 1 . (Hint: this is easy.) (4) Describe explicitly a smooth knot (image of a C 1 function with nonvanishing derivative) K in R3 so that the projection of K to R2 = {(x, y, 0)} ⊂ R3 has infinit ...
... (3) Let f : S 1 → R3 be a continuous, injective map. Prove that the image f (S 1 ) of f is homeomorphic to S 1 . (Hint: this is easy.) (4) Describe explicitly a smooth knot (image of a C 1 function with nonvanishing derivative) K in R3 so that the projection of K to R2 = {(x, y, 0)} ⊂ R3 has infinit ...
x2 +y2 = 25. We know the graph of this to be a
... x2 + y 2 = 25 as containing several functions. Note ...
... x2 + y 2 = 25 as containing several functions. Note ...
About Lie Groups
... (1) conjugation: Ψg : G → G, h 7→ Lg ◦ Rg−1 (h) = Rg−1 ◦ Lg (h) = ghg −1 . Each of these maps is smooth, and in fact they are all diffeomorphisms. The inverses of Lg , Rg , and Ψg are Lg−1 , Rg−1 , and Ψg−1 , respectively. They are also group homomorphisms, so they are Lie group isomorphisms. Also, ...
... (1) conjugation: Ψg : G → G, h 7→ Lg ◦ Rg−1 (h) = Rg−1 ◦ Lg (h) = ghg −1 . Each of these maps is smooth, and in fact they are all diffeomorphisms. The inverses of Lg , Rg , and Ψg are Lg−1 , Rg−1 , and Ψg−1 , respectively. They are also group homomorphisms, so they are Lie group isomorphisms. Also, ...
Geometry – Ch1 Vocabulary Crossword Clues Down: 1. 2.
... Geometry – Ch1 Vocabulary Crossword Clues Down: 1. A conclusion you reach using inductive reasoning 2. Coplanar lines that do not intersect 3. An angle more than 90 degrees 4. An example for which a conjecture is incorrect 5. An angle less than 90 degrees 6. When two lines intersect to form right an ...
... Geometry – Ch1 Vocabulary Crossword Clues Down: 1. A conclusion you reach using inductive reasoning 2. Coplanar lines that do not intersect 3. An angle more than 90 degrees 4. An example for which a conjecture is incorrect 5. An angle less than 90 degrees 6. When two lines intersect to form right an ...
1 Lecture 4 - Integration by parts
... the derivative of f w.r.t x, written df dx literally indicates the infinitesimal change in f compared to the infinitesimal change in x. But the operator “d” actually behaves like a derivative: given f (x) = x2 then df (x) = 2x dx. If we divide both sides by dx, we get df = 2x, dx which is the correc ...
... the derivative of f w.r.t x, written df dx literally indicates the infinitesimal change in f compared to the infinitesimal change in x. But the operator “d” actually behaves like a derivative: given f (x) = x2 then df (x) = 2x dx. If we divide both sides by dx, we get df = 2x, dx which is the correc ...
Course Narrative
... understanding of the concepts and connections among concepts in calculus. The two major themes are the derivative as a rate of change and the integral as an accumulation function. Technology is used throughout the course and students are taught how to use graphing calculators to help solve problems, ...
... understanding of the concepts and connections among concepts in calculus. The two major themes are the derivative as a rate of change and the integral as an accumulation function. Technology is used throughout the course and students are taught how to use graphing calculators to help solve problems, ...
Derivative of secant
... This is usually written in a different fashion; there are often many different ways of writing combinations of trigonometric functions. The standard way of writing this is: d sin x ...
... This is usually written in a different fashion; there are often many different ways of writing combinations of trigonometric functions. The standard way of writing this is: d sin x ...
Remarks on the Cartan Formula and Its Applications
... on Riemannian manifolds, complex manifolds and generalized complex manifolds. We would like to point out that such commutator formulas are essentially consequences of the classical Cartan formula for Lie derivative, but they have deep applications in geometry such as in studying the smoothness of de ...
... on Riemannian manifolds, complex manifolds and generalized complex manifolds. We would like to point out that such commutator formulas are essentially consequences of the classical Cartan formula for Lie derivative, but they have deep applications in geometry such as in studying the smoothness of de ...
BOOK REVIEW
... A Poisson bracket on a smooth manifold M is bilinear product f, g → {f, g} defined on the space C ∞ (M ) of all smooth functions on M such that the space C ∞ (M ) is a Lie algebra with respect this form and the Leibniz identity {f g, h} = f {g, h}+g{f, h} holds. In this case the manifold M is called ...
... A Poisson bracket on a smooth manifold M is bilinear product f, g → {f, g} defined on the space C ∞ (M ) of all smooth functions on M such that the space C ∞ (M ) is a Lie algebra with respect this form and the Leibniz identity {f g, h} = f {g, h}+g{f, h} holds. In this case the manifold M is called ...
Ph.D. Qualifying examination in topology Charles Frohman and
... B3) Let Wc = f(x; y; z; w) 2 R4 : xyz = cg and Yc = f(x; y; z; w) 2 R4 : xzw = cg. For what real numbers c is Yc a three-manifold? For what pairs (c1 ; c2 ) is Wc1 \ Yc2 a two-manifold. B4) Consider the one form ...
... B3) Let Wc = f(x; y; z; w) 2 R4 : xyz = cg and Yc = f(x; y; z; w) 2 R4 : xzw = cg. For what real numbers c is Yc a three-manifold? For what pairs (c1 ; c2 ) is Wc1 \ Yc2 a two-manifold. B4) Consider the one form ...
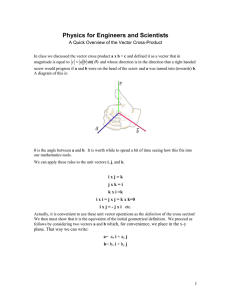
PHY-2049-003 Physics for Engineers and Scientists
... So the question is how do we get from these last two expressions to the ab sin() concept. Keep in mind that everything here is being done in the x-y plane just for simplicity. If you REALLY want to understand this most important process, follow the rest and then reproduce the calculations in all th ...
... So the question is how do we get from these last two expressions to the ab sin() concept. Keep in mind that everything here is being done in the x-y plane just for simplicity. If you REALLY want to understand this most important process, follow the rest and then reproduce the calculations in all th ...
Document
... If the points P and Q have position vectors r(t) and r(t + h), then represents the vector r(t + h) – r(t), which can therefore be regarded as a secant vector. If h > 0, the scalar multiple (1/h)(r(t + h) – r(t)) has the same direction as r(t + h) – r(t). As h 0, it appears that this vector approac ...
... If the points P and Q have position vectors r(t) and r(t + h), then represents the vector r(t + h) – r(t), which can therefore be regarded as a secant vector. If h > 0, the scalar multiple (1/h)(r(t + h) – r(t)) has the same direction as r(t + h) – r(t). As h 0, it appears that this vector approac ...
These are some math problems i need today if possible
... n times a year for t years at interest rate of r and initial deposit p is given by the following fromula below/ A=p{1+ r/n)^nt, gind the formula for A if the number of compounding periood per year becomes larger or n∞ ...
... n times a year for t years at interest rate of r and initial deposit p is given by the following fromula below/ A=p{1+ r/n)^nt, gind the formula for A if the number of compounding periood per year becomes larger or n∞ ...
Derivatives and Integrals of Vector Functions
... Solution: (a) According to Theorem 2, we differentiate each component of r: r ′(t) = 3t2i + (1 – t)e–t j + 2 cos 2t k ...
... Solution: (a) According to Theorem 2, we differentiate each component of r: r ′(t) = 3t2i + (1 – t)e–t j + 2 cos 2t k ...