Geometry review, part I Geometry review I
... ignored), but we have different properties. In 2D, the vector perpendicular to a given vector is unique (up to a scale). In 3D, it is not. Two 3D vectors in 3D can be multiplied to get a vector (vector or cross product). Dot product works the same way, but the coordinate expression is (v·w) = vxwx+ ...
... ignored), but we have different properties. In 2D, the vector perpendicular to a given vector is unique (up to a scale). In 3D, it is not. Two 3D vectors in 3D can be multiplied to get a vector (vector or cross product). Dot product works the same way, but the coordinate expression is (v·w) = vxwx+ ...
Background notes
... commutes. If ϕ has an inverse, then we say ϕ is an isomorphism of fiber bundles. In the diagram π1 : U × F → U is projection onto the first factor. (We will often use the notation πk : X1 × X2 × · · · × Xn → Xk for projection onto the kth factor of a Cartesian product.) The commutation of the diagra ...
... commutes. If ϕ has an inverse, then we say ϕ is an isomorphism of fiber bundles. In the diagram π1 : U × F → U is projection onto the first factor. (We will often use the notation πk : X1 × X2 × · · · × Xn → Xk for projection onto the kth factor of a Cartesian product.) The commutation of the diagra ...
02 Dot Product
... Now let’s explore what happens when a dot product is zero. We’ll check first in twodimensions again. So look at the vectors (3, 1) and (–2, 6). It is easy to check that their dot product is zero: 3⋅(–2) + 1⋅6 = 0. What geometric connection does this have? Look at the line segment along (3, 1). It ha ...
... Now let’s explore what happens when a dot product is zero. We’ll check first in twodimensions again. So look at the vectors (3, 1) and (–2, 6). It is easy to check that their dot product is zero: 3⋅(–2) + 1⋅6 = 0. What geometric connection does this have? Look at the line segment along (3, 1). It ha ...
Isotopy lemma. `Manifolds have no points. You can`t distinguish their
... Definition 0.1 An isotopy of M is a diffeomorphism φ of M which is homotopic to the identity, through diffeomorphisms. That is, there is a smooth map FM × I → M , with Ft : M → M a diffeomorphism for each t ∈ I, and F0 = Id, F1 = φ. We say two points, or two subsets of M are isotopic if there is an ...
... Definition 0.1 An isotopy of M is a diffeomorphism φ of M which is homotopic to the identity, through diffeomorphisms. That is, there is a smooth map FM × I → M , with Ft : M → M a diffeomorphism for each t ∈ I, and F0 = Id, F1 = φ. We say two points, or two subsets of M are isotopic if there is an ...
VECTOR ALGEBRA IMPORTANT POINTS TO REMEMBER A
... 3. Find the direction cosines of a vector which is equally inclined with OX, OY and OZ. If l l is given, find the total number of such vectors. 4. A vector is inclined at equal angles to OX, OY and OZ. If the magnitude of is 6 units, find 5. A vector has length 21 and d. r.s 2, -3, 6. Find the direc ...
... 3. Find the direction cosines of a vector which is equally inclined with OX, OY and OZ. If l l is given, find the total number of such vectors. 4. A vector is inclined at equal angles to OX, OY and OZ. If the magnitude of is 6 units, find 5. A vector has length 21 and d. r.s 2, -3, 6. Find the direc ...
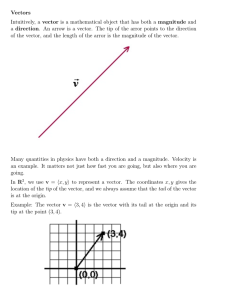
Vectors Intuitively, a vector is a mathematical object that has both a
... v = hx, yi always has its tail at the origin, the location of a vector is irrelevant. The reason we need to specify that its tail is at the origin is because we want to know to which direction that vector is pointing. Therefore, the vector v = h3, −1i (with its tail at the origin) and the vector w w ...
... v = hx, yi always has its tail at the origin, the location of a vector is irrelevant. The reason we need to specify that its tail is at the origin is because we want to know to which direction that vector is pointing. Therefore, the vector v = h3, −1i (with its tail at the origin) and the vector w w ...
Introduction to the Engineering Design Process
... – Sketch vector addition using parallelogram law – Determine interior angles from geometry of the problem (recall sum total of interior angles of parallelogram = 360°) – Label known angles and known forces – Redraw half portion of constructed parallelogram to show triangular head-to-tail addition co ...
... – Sketch vector addition using parallelogram law – Determine interior angles from geometry of the problem (recall sum total of interior angles of parallelogram = 360°) – Label known angles and known forces – Redraw half portion of constructed parallelogram to show triangular head-to-tail addition co ...
REPRESENTATIONS OF LIE GROUPS AND LIE ALGEBRAS
... with B the transition matrix between the two bases, it follows that the transition maps are smooth. Thus, this smooth manifold structure on GL(V ) is independent of the choice of basis. This Lie group GL(V ) will play an important role in the later sections of this paper. First we review the concept ...
... with B the transition matrix between the two bases, it follows that the transition maps are smooth. Thus, this smooth manifold structure on GL(V ) is independent of the choice of basis. This Lie group GL(V ) will play an important role in the later sections of this paper. First we review the concept ...
Answers
... We expand kv + wk2 using properties of the dot product: kv + wk2 = (v + w) · (v + w) =v·v+v·w+w·v+w·w = kvk2 + 2(v · w) + kwk2 (since v · w = w · v) = kvk2 + kwk2 (since v ⊥ w ⇔ v · w = 0) Thus, kv + wk2 = kvk2 + kwk2 , as promised. 12. Let A and B be endpoints of a diameter of a circle with a radi ...
... We expand kv + wk2 using properties of the dot product: kv + wk2 = (v + w) · (v + w) =v·v+v·w+w·v+w·w = kvk2 + 2(v · w) + kwk2 (since v · w = w · v) = kvk2 + kwk2 (since v ⊥ w ⇔ v · w = 0) Thus, kv + wk2 = kvk2 + kwk2 , as promised. 12. Let A and B be endpoints of a diameter of a circle with a radi ...
PDF
... 5. | · | : V → V given by |x| := −x ∨ x is continuous Proof. (1 ⇔ 2). If ∨ is continuous, then x ∧ y = x + y − x ∨ y is continuous too, as + and − are both continuous under a topological vector space. This proof works in reverse too. (1 ⇒ 3), (1 ⇒ 4), and (3 ⇔ 4) are obvious. To see (4 ⇒ 5), we see ...
... 5. | · | : V → V given by |x| := −x ∨ x is continuous Proof. (1 ⇔ 2). If ∨ is continuous, then x ∧ y = x + y − x ∨ y is continuous too, as + and − are both continuous under a topological vector space. This proof works in reverse too. (1 ⇒ 3), (1 ⇒ 4), and (3 ⇔ 4) are obvious. To see (4 ⇒ 5), we see ...
Introduction to Index Theory Notes
... the splitting principle, one may often assume that the vector bundle is a direct sum of line bundles; if one is able to prove an identity in the Chern classes by using this assumption, then the result is true in general. In any case, expressing characteristic classes in terms of the xk ’s instead of ...
... the splitting principle, one may often assume that the vector bundle is a direct sum of line bundles; if one is able to prove an identity in the Chern classes by using this assumption, then the result is true in general. In any case, expressing characteristic classes in terms of the xk ’s instead of ...
Chapter 2: Manifolds
... Then any element of the group can be written as g(a) where a = (a1 , · · · , an ) . Since the composition of two elements of G must be another element of G, we can write g(a)g(b) = g(φ(a, b)) where φ = (φ1 , · · · , φn ) are n functions of a and b. Then for a Lie group, the functions φ are smooth (r ...
... Then any element of the group can be written as g(a) where a = (a1 , · · · , an ) . Since the composition of two elements of G must be another element of G, we can write g(a)g(b) = g(φ(a, b)) where φ = (φ1 , · · · , φn ) are n functions of a and b. Then for a Lie group, the functions φ are smooth (r ...
symmetry properties of sasakian space forms
... let (φ, ξ, η) be tensor fields of type (1, 1), (1, 0) and (0, 1) respectively on M , such that: φ2 (X) = −X + η(X)ξ, η ◦ φ = 0, η(ξ) = 1, g(φX, φY ) = g(X, Y ) − η(X)η(Y ), for all vector field X, Y of M . If in addition, dη(X, Y ) = g(X, φY ), then M is called contact Riemannian manifold. If, moreo ...
... let (φ, ξ, η) be tensor fields of type (1, 1), (1, 0) and (0, 1) respectively on M , such that: φ2 (X) = −X + η(X)ξ, η ◦ φ = 0, η(ξ) = 1, g(φX, φY ) = g(X, Y ) − η(X)η(Y ), for all vector field X, Y of M . If in addition, dη(X, Y ) = g(X, φY ), then M is called contact Riemannian manifold. If, moreo ...
Ch 3: Motion in 2 and 3-D 3-1 The Displacement Vector DEF
... From unit circle geometry, and trig functions: The basic form of a circle, centered at the origin is given in: Rectangular coordinates as x 2 + y 2 = r2 Polar coordinates as cos2θ + sin2θ = 1 Based on some simple manipulations that you will address later on: x = r cos θ and y = r sin θ Further mani ...
... From unit circle geometry, and trig functions: The basic form of a circle, centered at the origin is given in: Rectangular coordinates as x 2 + y 2 = r2 Polar coordinates as cos2θ + sin2θ = 1 Based on some simple manipulations that you will address later on: x = r cos θ and y = r sin θ Further mani ...
Vectors - Fundamentals and Operations
... The parallelogram method of vector resolution involves using an accurately drawn, scaled vector diagram to determine the components of the vector. Briefly put, the method involves drawing the vector to scale in the indicated direction, sketching a parallelogram around the vector such that the vecto ...
... The parallelogram method of vector resolution involves using an accurately drawn, scaled vector diagram to determine the components of the vector. Briefly put, the method involves drawing the vector to scale in the indicated direction, sketching a parallelogram around the vector such that the vecto ...
VECTOR ADDITION
... In the experiment you will be given different forces. You will represent these forces by vectors of appropriate lengths by choosing a scale. Your first vector will always start from the origin with its tail at the origin and you draw this vector at the given angle. The tail of the second vector will ...
... In the experiment you will be given different forces. You will represent these forces by vectors of appropriate lengths by choosing a scale. Your first vector will always start from the origin with its tail at the origin and you draw this vector at the given angle. The tail of the second vector will ...
Lie Groups and Lie Algebras Presentation Fall 2014 Chiahui
... (a) The inclusion map S 1 → C∗ is a Lie group homomorphism. (b) Considering R as a Lie group under addition, and R∗ as a Lie group under multiplication, the map exp: R → R∗ given by exp(t) = et is smooth, and is a Lie group homomorphism because es+t = es et . The image of exp is the open subgroup R+ ...
... (a) The inclusion map S 1 → C∗ is a Lie group homomorphism. (b) Considering R as a Lie group under addition, and R∗ as a Lie group under multiplication, the map exp: R → R∗ given by exp(t) = et is smooth, and is a Lie group homomorphism because es+t = es et . The image of exp is the open subgroup R+ ...
Lesson Plan Format
... lists the ____________ and ____________ change from the initial point to the terminal point. The component form of is <2, 3>. ...
... lists the ____________ and ____________ change from the initial point to the terminal point. The component form of is <2, 3>. ...
Example 1: Solution: f P
... of f and g. This rule allows us to differentiate complicated functions in terms of known derivatives of simpler functions. The Chain Rule If g is a differentiable function at x and f is differentiable at g(x), then the composition function f g = f(g(x)) is differentiable at x. The derivative of the ...
... of f and g. This rule allows us to differentiate complicated functions in terms of known derivatives of simpler functions. The Chain Rule If g is a differentiable function at x and f is differentiable at g(x), then the composition function f g = f(g(x)) is differentiable at x. The derivative of the ...
Vectors Worksheet - WLPCS Upper School
... Vector addition is the process of finding the resultant vector when given the components of the vector. In one-dimensional vector addition, you will be working on either the x (horizontal) or y (vertical) axis. The vector addition is simply the addition (or subtraction if the vectors are in opposite ...
... Vector addition is the process of finding the resultant vector when given the components of the vector. In one-dimensional vector addition, you will be working on either the x (horizontal) or y (vertical) axis. The vector addition is simply the addition (or subtraction if the vectors are in opposite ...
PDF
... Essentially, given a finite dimensional abstract vector space, a choice of a coordinate frame (which is really the same thing as a basis) sets up a linear bijection between the abstract vectors and list vectors, and makes it possible to represent the one in terms of the other. The representation is ...
... Essentially, given a finite dimensional abstract vector space, a choice of a coordinate frame (which is really the same thing as a basis) sets up a linear bijection between the abstract vectors and list vectors, and makes it possible to represent the one in terms of the other. The representation is ...