Affine Decomposition of Isometries in Nilpotent Lie Groups
... dE to the Lie algebra. We take any point x ∈ B such that π(x) = x̃. Then indeed the points [nb] := πS (nb) (or actually a subsequence) eventually arrive to the open set π(B(x, ε)) 3 x̃. The conclusion ”thus for n ≥ nε there exists x0n ∈ B(x, ε). . . ” and the rest of the proof is correct and clear e ...
... dE to the Lie algebra. We take any point x ∈ B such that π(x) = x̃. Then indeed the points [nb] := πS (nb) (or actually a subsequence) eventually arrive to the open set π(B(x, ε)) 3 x̃. The conclusion ”thus for n ≥ nε there exists x0n ∈ B(x, ε). . . ” and the rest of the proof is correct and clear e ...
Affine Decomposition of Isometries in Nilpotent Lie Groups
... have more assumptions on the algebraic structure of the space, but Riemannian Lie groups have more assumptions on the metric structure than subRiemannian Carnot groups. Our setting of metric Lie groups is a generalization of the both. But to stress the logic, our proof of the general result actually ...
... have more assumptions on the algebraic structure of the space, but Riemannian Lie groups have more assumptions on the metric structure than subRiemannian Carnot groups. Our setting of metric Lie groups is a generalization of the both. But to stress the logic, our proof of the general result actually ...
MA352_Differential_Geometry_CIIT_VU
... There are many examples of vector field around us, for example, the gravitational field etc. In such vector fields each point of the domain space represents a vector, for example, in case of gravitation vector field each point of the space represents a vector, directed towards the center of the eart ...
... There are many examples of vector field around us, for example, the gravitational field etc. In such vector fields each point of the domain space represents a vector, for example, in case of gravitation vector field each point of the space represents a vector, directed towards the center of the eart ...
Print - Robert W. Gray
... exploration and analysis with a part of the whole, in contradistinction to synergetics' inauguration of exploration and analysis with total Universe, within which it discovers whole conceptual systems, within which it identifies subentities always dealing with experimentally discovered and experimen ...
... exploration and analysis with a part of the whole, in contradistinction to synergetics' inauguration of exploration and analysis with total Universe, within which it discovers whole conceptual systems, within which it identifies subentities always dealing with experimentally discovered and experimen ...
Suggested problems
... First, find any vector orthogonal to < 8, 1, 1 > using 8x + y + z = 0. Letting x = 1 and y = 1 gives z = −9, and so < 1, 1, −9 > is orthogonal to < 8, 1, 1 >. Normalizing gives ...
... First, find any vector orthogonal to < 8, 1, 1 > using 8x + y + z = 0. Letting x = 1 and y = 1 gives z = −9, and so < 1, 1, −9 > is orthogonal to < 8, 1, 1 >. Normalizing gives ...
1.5 Smooth maps
... Definition 1.32. A map f : M → N is called smooth when for each chart (U, φ) for M and each chart (V, ψ) for N , the composition ψ ◦ f ◦ φ−1 is a smooth map, i.e. ψ ◦ f ◦ φ−1 ∈ C ∞ (φ(U ), Rn ). The set of smooth maps (i.e. morphisms) from M to N is denoted C ∞ (M, N ). A smooth map with a smooth in ...
... Definition 1.32. A map f : M → N is called smooth when for each chart (U, φ) for M and each chart (V, ψ) for N , the composition ψ ◦ f ◦ φ−1 is a smooth map, i.e. ψ ◦ f ◦ φ−1 ∈ C ∞ (φ(U ), Rn ). The set of smooth maps (i.e. morphisms) from M to N is denoted C ∞ (M, N ). A smooth map with a smooth in ...
FROM INFINITESIMAL HARMONIC TRANSFORMATIONS TO RICCI
... Recall that a vector field ξ is an infinitesimal conformal transformation if Lξ g = −2n−1 (d∗ θ)g for θ = g(ξ, ·). By direct computation, we can deduce the equality ∆θ + (1 − 2/n)dd∗ θ = 2 Ric∗ ξ. Moreover, by virtue of the Lichnerowicz theorem (see [14]) this equality is a necessary and sufficient c ...
... Recall that a vector field ξ is an infinitesimal conformal transformation if Lξ g = −2n−1 (d∗ θ)g for θ = g(ξ, ·). By direct computation, we can deduce the equality ∆θ + (1 − 2/n)dd∗ θ = 2 Ric∗ ξ. Moreover, by virtue of the Lichnerowicz theorem (see [14]) this equality is a necessary and sufficient c ...
MATH 115 ACTIVITY 1:
... To extend our graphing techniques from last semester (intervals where f is increasing, inrevals where f is decreasing, etc.] to use with sine & cosine, we'd need to be able to solve equations like 3sin(2x) = 0. How many solutions are there to the equation sin(2x) = 0? What do they look like? ...
... To extend our graphing techniques from last semester (intervals where f is increasing, inrevals where f is decreasing, etc.] to use with sine & cosine, we'd need to be able to solve equations like 3sin(2x) = 0. How many solutions are there to the equation sin(2x) = 0? What do they look like? ...
Some applications of vector methods to plane geometry and plane
... Thus the laws which govern addition, subtraction, and scalar multiplication of v~tors are identic~1 wit~h those governing these operations In or4inary algebra2. Vectors are said to be collinear when parallel to the same line; vectors which lie in or are parallel to the same plane are coplanar. A vec ...
... Thus the laws which govern addition, subtraction, and scalar multiplication of v~tors are identic~1 wit~h those governing these operations In or4inary algebra2. Vectors are said to be collinear when parallel to the same line; vectors which lie in or are parallel to the same plane are coplanar. A vec ...
Vector Geometry for Computer Graphics
... Here t is a scalar parameter and p is an arbitrary point on the line. For example, suppose we need the equation of the line through points <2, 1, 3> and <4, 0, 5>. A vector parallel to this line is the vector from <2, 1, 3> to <4, 0, 5>, which is <4-2, 0-1, 5-3> = <2, -1, 2>. The line is then ...
... Here t is a scalar parameter and p is an arbitrary point on the line. For example, suppose we need the equation of the line through points <2, 1, 3> and <4, 0, 5>. A vector parallel to this line is the vector from <2, 1, 3> to <4, 0, 5>, which is <4-2, 0-1, 5-3> = <2, -1, 2>. The line is then ...
Vector Geometry for Computer Graphics
... Here t is a scalar parameter and p is an arbitrary point on the line. For example, suppose we need the equation of the line through points <2, 1, 3> and <4, 0, 5>. A vector parallel to this line is the vector from <2, 1, 3> to <4, 0, 5>, which is <4-2, 0-1, 5-3> = <2, -1, 2>. The line is then ...
... Here t is a scalar parameter and p is an arbitrary point on the line. For example, suppose we need the equation of the line through points <2, 1, 3> and <4, 0, 5>. A vector parallel to this line is the vector from <2, 1, 3> to <4, 0, 5>, which is <4-2, 0-1, 5-3> = <2, -1, 2>. The line is then ...
Vectors and Plane Geometry - University of Hawaii Mathematics
... in which order the additions are carried out, the result is the same. This property is called the associative law. In (3) we are saying that the addition of vectors is commutative, we may interchange the summands and the result is unchanged. In (4) we assert that there is a zero for the addition of ...
... in which order the additions are carried out, the result is the same. This property is called the associative law. In (3) we are saying that the addition of vectors is commutative, we may interchange the summands and the result is unchanged. In (4) we assert that there is a zero for the addition of ...
Transversal, Alternate Interior Angles, and Alternate Exterior Angles
... In this satellite view of a street, we can see many examples of transversals throughout the roads. They help people find ways to travel quicker using shortcuts through the roads. ...
... In this satellite view of a street, we can see many examples of transversals throughout the roads. They help people find ways to travel quicker using shortcuts through the roads. ...
Chapter 2
... Now using the coordinate direction angles, we can get UG, and determine G from the formula: G = 80UG lb. G = {80 ( cos (111°) i + cos (69.3°) j + cos (30.22°) k )} lb G = {- 28.67 i + 28.28 j + 69.13 k } lb Finally, find the resultant vector R = F + G or R = {6.69 i – 7.08 j + 156 k} lb ...
... Now using the coordinate direction angles, we can get UG, and determine G from the formula: G = 80UG lb. G = {80 ( cos (111°) i + cos (69.3°) j + cos (30.22°) k )} lb G = {- 28.67 i + 28.28 j + 69.13 k } lb Finally, find the resultant vector R = F + G or R = {6.69 i – 7.08 j + 156 k} lb ...
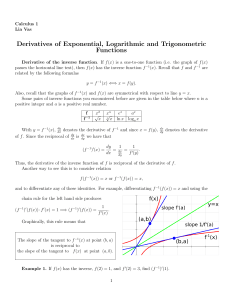
Derivative of General Exponential and Logarithmic
... derivatives of trigonometric, exponential & logarithmic functions ...
... derivatives of trigonometric, exponential & logarithmic functions ...
Group actions in symplectic geometry
... there is the following elementary result by Delzant [1]. If a connected semisimple Lie group G admits a Hamiltonian action on a closed symplectic manifold (M, ω) then it is compact. ...
... there is the following elementary result by Delzant [1]. If a connected semisimple Lie group G admits a Hamiltonian action on a closed symplectic manifold (M, ω) then it is compact. ...
2.1 Conditional Statements
... – b) converse – c) contrapositive If there is snow on the ground, then flowers are not in bloom. a) If there is no snow on the ground, then flowers are in bloom. b) If flowers are not in bloom, then there is snow on the ground. c) If flowers are in bloom, then there is no snow on the ground. ...
... – b) converse – c) contrapositive If there is snow on the ground, then flowers are not in bloom. a) If there is no snow on the ground, then flowers are in bloom. b) If flowers are not in bloom, then there is snow on the ground. c) If flowers are in bloom, then there is no snow on the ground. ...
On a class of transformation groups
... (X, qn(S) ) is locally arewise connected,it follows by (3) (X, 9i (S)) map of from (2) that f is a conltinuous (f5: 971 (5f) ) x ...
... (X, qn(S) ) is locally arewise connected,it follows by (3) (X, 9i (S)) map of from (2) that f is a conltinuous (f5: 971 (5f) ) x ...
Use the Geometry Calculator
... vectors. In drawings, points are displayed as dots, and vectors are displayed as lines with arrows. CAL supports points expressed in all AutoCAD formats. ...
... vectors. In drawings, points are displayed as dots, and vectors are displayed as lines with arrows. CAL supports points expressed in all AutoCAD formats. ...
x and y - Ninova
... The distance between two points In a Euclidean space we define the distance between two points p and q as the norm of the vector p – q. Because points correspond to vectors, for a fixed origin, and vectors correspond to column matrices, for a fixed basis, there is also a one-to-one correspondence b ...
... The distance between two points In a Euclidean space we define the distance between two points p and q as the norm of the vector p – q. Because points correspond to vectors, for a fixed origin, and vectors correspond to column matrices, for a fixed basis, there is also a one-to-one correspondence b ...
Normed vector space
... is a seminorm on the vector space of all functions on which the Lebesgue integral on the right hand side is defined and finite. However, the seminorm is equal to zero for any function supported on a set of Lebesgue measure zero. These functions form a subspace which we "quotient out", making them eq ...
... is a seminorm on the vector space of all functions on which the Lebesgue integral on the right hand side is defined and finite. However, the seminorm is equal to zero for any function supported on a set of Lebesgue measure zero. These functions form a subspace which we "quotient out", making them eq ...