10-10 Viscosity
... •Internal friction of a fluid is called viscosity. •Grease is more viscous than oil which is more viscous than gasoline…different fluids posess an intrinsic viscosity indicated by their coefficient of viscosity (h) …or eta. See pg 295. •F= hA(v/l) A=area…v=velocity…l = length or linear location from ...
... •Internal friction of a fluid is called viscosity. •Grease is more viscous than oil which is more viscous than gasoline…different fluids posess an intrinsic viscosity indicated by their coefficient of viscosity (h) …or eta. See pg 295. •F= hA(v/l) A=area…v=velocity…l = length or linear location from ...
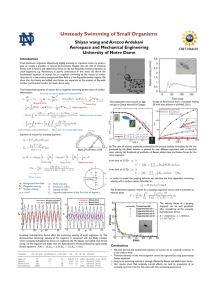
Unsteady Swimming of Small Organisms
... Small planktonic organisms ubiquitously display unsteady or impulsive motion to attack a prey or escape a predator in natural environments. Despite this, the role of unsteady forces such as history and added mass forces on the low Reynolds number propulsion of small organisms, e.g. Paramecium, is po ...
... Small planktonic organisms ubiquitously display unsteady or impulsive motion to attack a prey or escape a predator in natural environments. Despite this, the role of unsteady forces such as history and added mass forces on the low Reynolds number propulsion of small organisms, e.g. Paramecium, is po ...
Waves and Vibrations - Cardinal Newman
... A full mathematical description of the wave describes the displacement of any point as a function of both distance and time: ...
... A full mathematical description of the wave describes the displacement of any point as a function of both distance and time: ...
Waves - Websupport1
... The brown curve is a “snapshot” of the wave at some instant in time The blue curve is later in time The high points are crests of the wave The low points are troughs of the wave ...
... The brown curve is a “snapshot” of the wave at some instant in time The blue curve is later in time The high points are crests of the wave The low points are troughs of the wave ...
Name - WordPress.com
... o Resting point (line) o Positive amplitude o Negative amplitude o Period Wave Characteristics Amplitude—maximum height or depth a crest or trough moves from a resting point or line o Crest --- positive distance from resting point (compare long vs. transverse) o Trough --- negative distance from a ...
... o Resting point (line) o Positive amplitude o Negative amplitude o Period Wave Characteristics Amplitude—maximum height or depth a crest or trough moves from a resting point or line o Crest --- positive distance from resting point (compare long vs. transverse) o Trough --- negative distance from a ...
Final exam review1
... The earth exerts the necessary centripetal force on an orbiting satellite to keep it moving in a circle at constant speed. Which statement best explains why the speed of the satellite does not change even though there is a net force exerted on it? a. The satellite is in equilibrium. b. The accelera ...
... The earth exerts the necessary centripetal force on an orbiting satellite to keep it moving in a circle at constant speed. Which statement best explains why the speed of the satellite does not change even though there is a net force exerted on it? a. The satellite is in equilibrium. b. The accelera ...
Lecture 26 - Wednesday June 3rd
... γ, and positive if the fluid tends to flow with γ. Stokes’ Theorem relates the circulation of a fluid around a curve γ forming the boundary of a surface with the tendency to rotate around normal axes to the surface: Stokes’ Theorem. Let Σ be an oriented surface with boundary γ and let f be C 1 (Σ). ...
... γ, and positive if the fluid tends to flow with γ. Stokes’ Theorem relates the circulation of a fluid around a curve γ forming the boundary of a surface with the tendency to rotate around normal axes to the surface: Stokes’ Theorem. Let Σ be an oriented surface with boundary γ and let f be C 1 (Σ). ...
4 METHODS TO CALCULATE THE 2D POTENTIAL COEFFICIENTS
... (A) Methods Based on the Conformal Mapping and Ursell Theory (a1) Circular Cylinder: Ursell (1949) solved the linear boundary value problem of the circular cylinder oscillating on the free surface. The velocity potential is represented as a sum of an infinite set of multi poles satisfying the free s ...
... (A) Methods Based on the Conformal Mapping and Ursell Theory (a1) Circular Cylinder: Ursell (1949) solved the linear boundary value problem of the circular cylinder oscillating on the free surface. The velocity potential is represented as a sum of an infinite set of multi poles satisfying the free s ...
Unit 3 Lesson 2
... • Another property is wave period, the time required for one wavelength to pass a given point. • Frequency is also a way to express how far apart waves are in time. It is the number of crests that pass a point in a certain amount of time. ...
... • Another property is wave period, the time required for one wavelength to pass a given point. • Frequency is also a way to express how far apart waves are in time. It is the number of crests that pass a point in a certain amount of time. ...
Powerpoint Format ()
... 23.7, Thin Lenses and Refraction Theory, plus lab materials from this semester. A masteringphysics Problem Set is due Friday by 5:00 PM. It is the last problem set of 2007. Suggested Chapter 23 Exercises and Problems for Practice: 11, 17, 19, 27, 39, 49, 73, 81 ...
... 23.7, Thin Lenses and Refraction Theory, plus lab materials from this semester. A masteringphysics Problem Set is due Friday by 5:00 PM. It is the last problem set of 2007. Suggested Chapter 23 Exercises and Problems for Practice: 11, 17, 19, 27, 39, 49, 73, 81 ...
PSB Final Review
... 2. The direction and length of a straight line from the starting point to the ending point of an object’s motion is ____________________. 3. Displacement and velocity are examples of ____________________ because they have both magnitude and direction. 4. Speed is measured in units of _______________ ...
... 2. The direction and length of a straight line from the starting point to the ending point of an object’s motion is ____________________. 3. Displacement and velocity are examples of ____________________ because they have both magnitude and direction. 4. Speed is measured in units of _______________ ...
2005 Pearson Prentice Hall This work is protected by
... A full mathematical description of the wave describes the displacement of any point as a function of both distance and time: ...
... A full mathematical description of the wave describes the displacement of any point as a function of both distance and time: ...
Wave Data Analysis and Statistics Jun 2015
... analysis provides a method to examine the energy level of a range of wave periods. Using spectral analysis it is therefore possible to determine the period of the waves with the most energy. This statistic, known as TP1, provides a more representative wave period for ocean waves than the zero crossi ...
... analysis provides a method to examine the energy level of a range of wave periods. Using spectral analysis it is therefore possible to determine the period of the waves with the most energy. This statistic, known as TP1, provides a more representative wave period for ocean waves than the zero crossi ...
Linear Algebra
... layer x y and 2 x 2 2 y 2 . Distances in the x direction over which the velocity varies appreciably are of order L, but those of the y direction are of order δ, which is much smaller than L. o u v Schematic of airfoil without and with circulation: ...
... layer x y and 2 x 2 2 y 2 . Distances in the x direction over which the velocity varies appreciably are of order L, but those of the y direction are of order δ, which is much smaller than L. o u v Schematic of airfoil without and with circulation: ...
Hint: Convert miles into nautical miles
... as the product of a number between one and ten and a power of ten. For example, the total surface area of the world’s oceans is approximately 143,000,000 square miles. To write this in scientific notation, first, move the decimal point left until you have a number between 1 and 10 (1.43). Then, coun ...
... as the product of a number between one and ten and a power of ten. For example, the total surface area of the world’s oceans is approximately 143,000,000 square miles. To write this in scientific notation, first, move the decimal point left until you have a number between 1 and 10 (1.43). Then, coun ...
Week 6
... Friction between the air and water transfers energy from the air to the water. When air blows over the water steadily along a given direction it sets ocean currents in motion. Winds are also responsible for creating most of the ocean waves we see. If winds really do drive ocean currents, what patter ...
... Friction between the air and water transfers energy from the air to the water. When air blows over the water steadily along a given direction it sets ocean currents in motion. Winds are also responsible for creating most of the ocean waves we see. If winds really do drive ocean currents, what patter ...
Chapter 8
... -A particular type of periodic motion is Simple Harmonic Motion (SHM). -Simple harmonic motion occurs when the net force along the direction of motion is a Hooke’s law type of force-that is, when the net force is linearly proportional to the magnitude of the system's displacement from equilibrium an ...
... -A particular type of periodic motion is Simple Harmonic Motion (SHM). -Simple harmonic motion occurs when the net force along the direction of motion is a Hooke’s law type of force-that is, when the net force is linearly proportional to the magnitude of the system's displacement from equilibrium an ...
Stokes wave
In fluid dynamics, a Stokes wave is a non-linear and periodic surface wave on an inviscid fluid layer of constant mean depth.This type of modelling has its origins in the mid 19th century when Sir George Stokes – using a perturbation series approach, now known as the Stokes expansion – obtained approximate solutions for non-linear wave motion.Stokes' wave theory is of direct practical use for waves on intermediate and deep water. It is used in the design of coastal and offshore structures, in order to determine the wave kinematics (free surface elevation and flow velocities). The wave kinematics are subsequently needed in the design process to determine the wave loads on a structure. For long waves (as compared to depth) – and using only a few terms in the Stokes expansion – its applicability is limited to waves of small amplitude. In such shallow water, a cnoidal wave theory often provides better periodic-wave approximations.While, in the strict sense, Stokes wave refers to progressive periodic waves of permanent form, the term is also used in connection with standing waves and even for random waves.