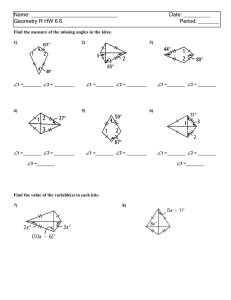
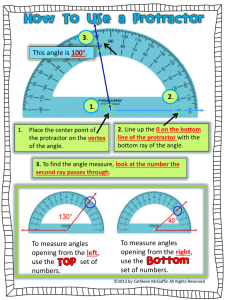
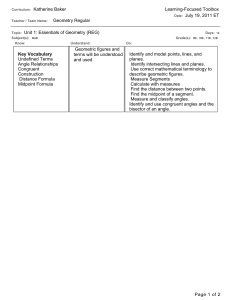
Chapter 7: Hyperbolic Geometry
... 1. A straight line may be drawn from a point to any other point. 2. A finite straight line may be produced to any length. 3. A circle may be described with any center and any radius. 4. All right angles are equal. 5. If a straight line meet two other straight lines so that as to make the interior an ...
... 1. A straight line may be drawn from a point to any other point. 2. A finite straight line may be produced to any length. 3. A circle may be described with any center and any radius. 4. All right angles are equal. 5. If a straight line meet two other straight lines so that as to make the interior an ...
Euclidean and Non-Euclidean Geometries: Development and History
... • “The effect of the discovery of hyperbolic geometry on our ideas of truth and reality have been so profound,” wrote the great Canadian geometer H.S.M. Coxeter, “that we can hardly imagine how shocking the possibility of a geometry different from Euclid’s must have seemed in 1820.” ...
... • “The effect of the discovery of hyperbolic geometry on our ideas of truth and reality have been so profound,” wrote the great Canadian geometer H.S.M. Coxeter, “that we can hardly imagine how shocking the possibility of a geometry different from Euclid’s must have seemed in 1820.” ...
Complex Bordism (Lecture 5)
... Remark 5. In the setting of Definition 2, it suffices to check the condition at one point x in each connected component of X. Our next goal is to show that if E is a complex-oriented cohomology theory, then all complex vector bundles have a canonical E-orientation. To prove this, it suffices to cons ...
... Remark 5. In the setting of Definition 2, it suffices to check the condition at one point x in each connected component of X. Our next goal is to show that if E is a complex-oriented cohomology theory, then all complex vector bundles have a canonical E-orientation. To prove this, it suffices to cons ...
World Globe
... • Lines extend indefinitely • All points equidistant from a given point in a plane form a circle ...
... • Lines extend indefinitely • All points equidistant from a given point in a plane form a circle ...
Euclidean vs Non-Euclidean Geometry
... from each other even if extended to infinity, and are known as parallels. In hyperbolic geometry they "curve away" from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often called ultraparallels. In ellipt ...
... from each other even if extended to infinity, and are known as parallels. In hyperbolic geometry they "curve away" from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often called ultraparallels. In ellipt ...
on geometry!
... 1.Take good notes and follow along mentally. 2.Make note cards for definitions, postulates and theorems 3.Try to do each assignment with little help. 4.Frequently study notes and go over old work. 5.Do not waste time in class. ...
... 1.Take good notes and follow along mentally. 2.Make note cards for definitions, postulates and theorems 3.Try to do each assignment with little help. 4.Frequently study notes and go over old work. 5.Do not waste time in class. ...
GR in a Nutshell
... The standard choice for a connection in standard GR is the LeviCivita connection, sometimes called “Christoffel symbols.” We get this connection if we start with a metric and assume the connection is torsion-free (and also “metric-compatible”). Now we are supposing the connection might not be torsio ...
... The standard choice for a connection in standard GR is the LeviCivita connection, sometimes called “Christoffel symbols.” We get this connection if we start with a metric and assume the connection is torsion-free (and also “metric-compatible”). Now we are supposing the connection might not be torsio ...