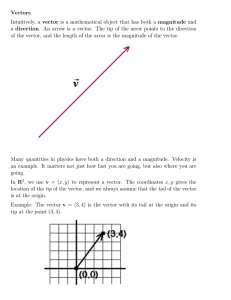
Week_1_LinearAlgebra..
... • If the spanning set is linearly independent, it’s also known as a basis for that subspace • The coordinate representation of a vector in a subspace is unique with respect to a basis for that subspace ...
... • If the spanning set is linearly independent, it’s also known as a basis for that subspace • The coordinate representation of a vector in a subspace is unique with respect to a basis for that subspace ...
Describing three-dimensional structures with spherical and
... discussed above, it is this vector whose plunge describes the apparent dip of a given bedding plane within a given cross-section plane. The cross product can be visualized using your right hand. Point the fingers of your right hand in the direction of the first vector, below called U. Now curl your ...
... discussed above, it is this vector whose plunge describes the apparent dip of a given bedding plane within a given cross-section plane. The cross product can be visualized using your right hand. Point the fingers of your right hand in the direction of the first vector, below called U. Now curl your ...
Chapter 3: Vectors in 2 and 3 Dimensions
... and angles in the plane and three dimension space. A more detailed profile of Euclid is given in the next section. n ...
... and angles in the plane and three dimension space. A more detailed profile of Euclid is given in the next section. n ...
Chapter 4, General Vector Spaces Section 4.1, Real Vector Spaces
... Chapter 4, General Vector Spaces Section 4.1, Real Vector Spaces In this chapter we will call objects that satisfy a set of axioms as vectors. This can be thought as generalizing the idea of vectors to a class of objects. Vector space axioms: Definition: Let V be an arbitrary nonempty set of objects ...
... Chapter 4, General Vector Spaces Section 4.1, Real Vector Spaces In this chapter we will call objects that satisfy a set of axioms as vectors. This can be thought as generalizing the idea of vectors to a class of objects. Vector space axioms: Definition: Let V be an arbitrary nonempty set of objects ...
PDF version of lecture with all slides
... Cross-‐product of two vectors The cross product a × b is defined as a vector c that is perpendicular to both a and b, with a direc>on given by the right-‐hand rule and a magnitude equal t ...
... Cross-‐product of two vectors The cross product a × b is defined as a vector c that is perpendicular to both a and b, with a direc>on given by the right-‐hand rule and a magnitude equal t ...
Summary of week 6 (lectures 16, 17 and 18) Every complex number
... (where (u1 , u2 , . . . , un ) is any orthogonal basis for U ) that P is a linear map. We can use orthogonal projections to show that every finite-dimensional inner product space has an orthogonal basis. More generally, suppose that V is an inner product space and U1 ⊂ U2 ⊂ · · · Ud is an increasing ...
... (where (u1 , u2 , . . . , un ) is any orthogonal basis for U ) that P is a linear map. We can use orthogonal projections to show that every finite-dimensional inner product space has an orthogonal basis. More generally, suppose that V is an inner product space and U1 ⊂ U2 ⊂ · · · Ud is an increasing ...
Revision 07/05/06
... announced that they were going to being working on the multiplication of matrices, and challenged the students to find the product of two 3 x 3 matrices: ...
... announced that they were going to being working on the multiplication of matrices, and challenged the students to find the product of two 3 x 3 matrices: ...
CS B659: Principles of Intelligent Robot Motion
... calculations (out of the realm of pure thought) as a displacement vector from some special reference point O, called the origin • The representation of a point P changes depending on the choice of O • When comparing or manipulating two points, their representations as vectors must use the same origi ...
... calculations (out of the realm of pure thought) as a displacement vector from some special reference point O, called the origin • The representation of a point P changes depending on the choice of O • When comparing or manipulating two points, their representations as vectors must use the same origi ...
Appendix A: Linear Algebra: Vectors
... products, such as the cross or outer product, which are important in many applications such as fluid mechanics and nonlinear dynamics. They are not treated here because they are not defined when going from vectors to matrices. Furthermore they are not easily generalized for vectors of order beyond 3 ...
... products, such as the cross or outer product, which are important in many applications such as fluid mechanics and nonlinear dynamics. They are not treated here because they are not defined when going from vectors to matrices. Furthermore they are not easily generalized for vectors of order beyond 3 ...
math 67a hw 2 solutions
... 4.4 Give an example of a non-empty subset U ⇢ R2 such that U is closed under scalar multiplication but is not a subspace of R2 Solution Define U to be the union of the x and y-axes; i.e., all points with x or y component zero. This set is closed under scalar multiplication because the product of any ...
... 4.4 Give an example of a non-empty subset U ⇢ R2 such that U is closed under scalar multiplication but is not a subspace of R2 Solution Define U to be the union of the x and y-axes; i.e., all points with x or y component zero. This set is closed under scalar multiplication because the product of any ...
Sections 3.4-3.6
... A vector space so large that no finite set of vectors spans it is called infinitedimensional. The Dimension of the Column Space of a Matrix Column Space of a Matrix: The pivot columns of a matrix A form a basis for ColA. Then the dimension of the column space, denoted dim(ColA), is the number of pi ...
... A vector space so large that no finite set of vectors spans it is called infinitedimensional. The Dimension of the Column Space of a Matrix Column Space of a Matrix: The pivot columns of a matrix A form a basis for ColA. Then the dimension of the column space, denoted dim(ColA), is the number of pi ...
Math 304–504 Linear Algebra Lecture 24: Orthogonal subspaces.
... Definition. Let U, V be subspaces of a vector space W . We say that W is a direct sum of U and V (denoted W = U ⊕ V ) if any w ∈ W is uniquely represented as w = u + v, where u ∈ U and v ∈ V . Remark. Given subspaces U, V ⊂ W , we can define a set U + V = {u + v | u ∈ U, v ∈ V }, which is also a sub ...
... Definition. Let U, V be subspaces of a vector space W . We say that W is a direct sum of U and V (denoted W = U ⊕ V ) if any w ∈ W is uniquely represented as w = u + v, where u ∈ U and v ∈ V . Remark. Given subspaces U, V ⊂ W , we can define a set U + V = {u + v | u ∈ U, v ∈ V }, which is also a sub ...
Cross product
In mathematics and vector calculus, the cross product or vector product (occasionally directed area product to emphasize the geometric significance) is a binary operation on two vectors in three-dimensional space (R3) and is denoted by the symbol ×. The cross product a × b of two linearly independent vectors a and b is a vector that is perpendicular to both and therefore normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with dot product (projection product).If two vectors have the same direction (or have the exact opposite direction from one another, i.e. are not linearly independent) or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two perpendicular vectors is the product of their lengths. The cross product is anticommutative (i.e. a × b = −b × a) and is distributive over addition (i.e. a × (b + c) = a × b + a × c). The space R3 together with the cross product is an algebra over the real numbers, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on a choice of orientation or ""handedness"". The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. Also, using the orientation and metric structure just as for the traditional 3-dimensional cross product, one can in n dimensions take the product of n − 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions. If one adds the further requirement that the product be uniquely defined, then only the 3-dimensional cross product qualifies. (See § Generalizations, below, for other dimensions.)























