LECT. 2 STRUCTURAL GEOL
... CALCULATION OF STRESS - STRAIN STRESS = FORCE/AREA STRAIN = L change/L STRAIN – CHANGE IN SHAPE OR SIZE OF A BODY CAUSED BY STRESS. ...
... CALCULATION OF STRESS - STRAIN STRESS = FORCE/AREA STRAIN = L change/L STRAIN – CHANGE IN SHAPE OR SIZE OF A BODY CAUSED BY STRESS. ...
Technical terms-3
... The transition from ductile to brittle behavior with a decrease in temperature exhibited by BCC alloys; the temperature range over which the transition occurs is determined by Charpy and Izod impact tests. Ductility A measure of a material’s ability to undergo appreciable plastic deformation before ...
... The transition from ductile to brittle behavior with a decrease in temperature exhibited by BCC alloys; the temperature range over which the transition occurs is determined by Charpy and Izod impact tests. Ductility A measure of a material’s ability to undergo appreciable plastic deformation before ...
HMWK_5
... We will use a cylinder (2 orientations) and two disks. We will tow each at 6-8 velocities and measure the force the strain the object applies on a strain gauge. This strain is proportional to the drag force the object experience, and the instrument measuring the strain provide an output that is prop ...
... We will use a cylinder (2 orientations) and two disks. We will tow each at 6-8 velocities and measure the force the strain the object applies on a strain gauge. This strain is proportional to the drag force the object experience, and the instrument measuring the strain provide an output that is prop ...
Brittle Fracture of Ceramics
... For compressive stresses, there is no stress amplification associated with any existent flaws. For this reason, brittle ceramics display much higher strengths in compression than in tension (on the order of a factor of 10), and they are generally utilized when load conditions are compressive. Flexur ...
... For compressive stresses, there is no stress amplification associated with any existent flaws. For this reason, brittle ceramics display much higher strengths in compression than in tension (on the order of a factor of 10), and they are generally utilized when load conditions are compressive. Flexur ...
Lecture 7 Mechanical Properties of Rocks
... unit weight of water= 62.4 pcf (lbs/ft3) for most rocks, gamma = 120 to 200 pcf. ...
... unit weight of water= 62.4 pcf (lbs/ft3) for most rocks, gamma = 120 to 200 pcf. ...
Structural Geology Stress and Strain
... – Force applied suddenly not allowing atoms time to shift or move in response to force ...
... – Force applied suddenly not allowing atoms time to shift or move in response to force ...
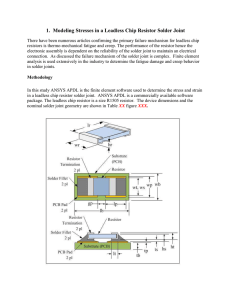
Project_FEA.doc
... that involve strain and temperature effect including solder joints and high temperature creep [ANSYS]. The Anand model does not require and explicit yield condition and loading /unloading criteria. It assumes that plastic flow occurs at all non-zero stress values. The Anand model represents the non- ...
... that involve strain and temperature effect including solder joints and high temperature creep [ANSYS]. The Anand model does not require and explicit yield condition and loading /unloading criteria. It assumes that plastic flow occurs at all non-zero stress values. The Anand model represents the non- ...
Lecture 8a - States of Matter
... object will still return to its original shape up to the elastic limit. Beyond the elastic limit, the material is permanently deformed, and it breaks at the breaking point. ...
... object will still return to its original shape up to the elastic limit. Beyond the elastic limit, the material is permanently deformed, and it breaks at the breaking point. ...
1 PHYSICS 231 Lecture 21: Some material science
... Stress: Tells something about the force causing the deformation Strain: Measure of the degree of deformation For small stress, strain and stress are linearly correlated. Strain = Constant*Stress Constant: elastic modulus The elastic modulus depends on: • Material that is deformed • Type of deformati ...
... Stress: Tells something about the force causing the deformation Strain: Measure of the degree of deformation For small stress, strain and stress are linearly correlated. Strain = Constant*Stress Constant: elastic modulus The elastic modulus depends on: • Material that is deformed • Type of deformati ...
Chapter 6: Mechanical Properties
... Testing of specimens stacked one on top of another is not recommended. ...
... Testing of specimens stacked one on top of another is not recommended. ...
Physics 130 - University of North Dakota
... Hooke’s Law = Simple Harmonic Motion Force always points toward the equilibrium position. ...
... Hooke’s Law = Simple Harmonic Motion Force always points toward the equilibrium position. ...
Compression The mechanical properties of a ductile metal are
... This causes a non uniformity of stress distribution, and conical sections of material at each end are strained and hardened to a lesser degree than the central region. The effect on the load – compression curve, after the smaller values of plastic strain have been achieved, is a fairly rapid rise in ...
... This causes a non uniformity of stress distribution, and conical sections of material at each end are strained and hardened to a lesser degree than the central region. The effect on the load – compression curve, after the smaller values of plastic strain have been achieved, is a fairly rapid rise in ...
Stress
... The change in stress field (caused by the effect of external forces) results in the displacement of particles inside the body which appears in the form of deformation (the change of shape and/or volume). The deformation is described by the so-called strain which quantifies the relative displacement ...
... The change in stress field (caused by the effect of external forces) results in the displacement of particles inside the body which appears in the form of deformation (the change of shape and/or volume). The deformation is described by the so-called strain which quantifies the relative displacement ...
Department of Civil Engineering
... Extension was observed over a gauge length of 200 mm wherein the original diameter was 15 mm. Plot the stress-strain curve and determine modulus of elasticity, yield strength, failure strain, and ultimate strength of the material. Did strain hardening occur, and did the material exhibit ductility? ...
... Extension was observed over a gauge length of 200 mm wherein the original diameter was 15 mm. Plot the stress-strain curve and determine modulus of elasticity, yield strength, failure strain, and ultimate strength of the material. Did strain hardening occur, and did the material exhibit ductility? ...
Spring Forces and Simple Harmonic Motion
... Strain is the change in a dimensional quantity expressed as a fraction of its un-deformed value: ...
... Strain is the change in a dimensional quantity expressed as a fraction of its un-deformed value: ...
Important Engineering and HydroGeologic Properties of
... Under relatively low loads of relatively short duration, nearly all solid materials, including rocks, deform in a recoverable manner. In other words, if the loads are relaxed, the material rebounds to its original shape. This is called elastic deformation. Under sufficiently large loads or over suff ...
... Under relatively low loads of relatively short duration, nearly all solid materials, including rocks, deform in a recoverable manner. In other words, if the loads are relaxed, the material rebounds to its original shape. This is called elastic deformation. Under sufficiently large loads or over suff ...
Mechanical Properties of Metals
... Learn basic concepts for metals, which have the simplest behavior Return to it later when we study ceramics, polymers, composite materials, nanotubes ...
... Learn basic concepts for metals, which have the simplest behavior Return to it later when we study ceramics, polymers, composite materials, nanotubes ...
Calculating the impact force of a mass on an elastic
... done deal and we needn’t worry about the exact magnitude of the ensuing deformation and the relative amounts of plastic deformation. So, back to this deflection u: after the mass contacts the structure it deforms the structure by an amount that depends upon the stiffness of the structure. Treat the ...
... done deal and we needn’t worry about the exact magnitude of the ensuing deformation and the relative amounts of plastic deformation. So, back to this deflection u: after the mass contacts the structure it deforms the structure by an amount that depends upon the stiffness of the structure. Treat the ...
CTE3-Script.pdf
... particles of the body. Specifically, σxy is the component of the stress tensor representing force along the x direction acting on a plane whose normal is y and x . All other stress tensor components are defined similarly. The last term are the components ρfx , ρfy , ρfz of volume forces acting on th ...
... particles of the body. Specifically, σxy is the component of the stress tensor representing force along the x direction acting on a plane whose normal is y and x . All other stress tensor components are defined similarly. The last term are the components ρfx , ρfy , ρfz of volume forces acting on th ...
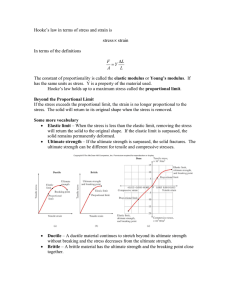
Hooke`s law in terms of stress and strain is strain stress∝ In terms of
... Other Deformations There are other ways to deform a solid. Two additional ways are shear deformation and volume deformation. Shear Deformation The forces act parallel to the edge of the solid. Tensile and compressive forces act perpendicular to the edges. ...
... Other Deformations There are other ways to deform a solid. Two additional ways are shear deformation and volume deformation. Shear Deformation The forces act parallel to the edge of the solid. Tensile and compressive forces act perpendicular to the edges. ...
Stress - Delta University!
... Shear is the result of two sets of forces directed towards each other but not in the same straight line.(fig.3) Torsion It results from the twisting of the body. (fig.3) Bending It results by applying bending movement.(fig.3) ...
... Shear is the result of two sets of forces directed towards each other but not in the same straight line.(fig.3) Torsion It results from the twisting of the body. (fig.3) Bending It results by applying bending movement.(fig.3) ...
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.A deformation may be caused by external loads, body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc.Strain is a description of deformation in terms of relative displacement of particles in the body that excludes rigid-body motions. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered.In a continuous body, a deformation field results from a stress field induced by applied forces or is due to changes in the temperature field inside the body. The relation between stresses and induced strains is expressed by constitutive equations, e.g., Hooke's law for linear elastic materials. Deformations which are recovered after the stress field has been removed are called elastic deformations. In this case, the continuum completely recovers its original configuration. On the other hand, irreversible deformations remain even after stresses have been removed. One type of irreversible deformation is plastic deformation, which occurs in material bodies after stresses have attained a certain threshold value known as the elastic limit or yield stress, and are the result of slip, or dislocation mechanisms at the atomic level. Another type of irreversible deformation is viscous deformation, which is the irreversible part of viscoelastic deformation.In the case of elastic deformations, the response function linking strain to the deforming stress is the compliance tensor of the material.