Chapter 19
... molecules in a substance is its internal (or thermal) energy. Temperature: measures molecules’ average kinetic energy Internal energy: total energy of all molecules Heat: transfer of energy due to difference in ...
... molecules in a substance is its internal (or thermal) energy. Temperature: measures molecules’ average kinetic energy Internal energy: total energy of all molecules Heat: transfer of energy due to difference in ...
4. Classical Thermodynamics
... electric field and polarization for a dielectric. In what follows we’ll assume that we’re dealing with a gas and use p and V to specify the state. Everything that we say can be readily extended to more general settings. So far, we don’t have a definition of temperature. This is provided by the zerot ...
... electric field and polarization for a dielectric. In what follows we’ll assume that we’re dealing with a gas and use p and V to specify the state. Everything that we say can be readily extended to more general settings. So far, we don’t have a definition of temperature. This is provided by the zerot ...
8.044 Lecture Notes Chapter 9: Quantum Ideal Gases
... [This section is about quantum mechanics. You’ve already encountered some of these ideas in 8.04, and will discuss this further in 8.05. We’ll come back in subsection 9.4 and think about when this business reduces to classical mechanics.] Consider two particles. Their state can be described by a wav ...
... [This section is about quantum mechanics. You’ve already encountered some of these ideas in 8.04, and will discuss this further in 8.05. We’ll come back in subsection 9.4 and think about when this business reduces to classical mechanics.] Consider two particles. Their state can be described by a wav ...
Essay 1: Pressure and Forces Pressure and Forces
... a gas consists of molecules which do interact very poorly. If one forgets about any electrostatic or intermolecular attractive forces between the molecules, one can assume that all collisions are perfectly elastic. One can visualize the gas as a collection of perfectly hard spheres which collide but ...
... a gas consists of molecules which do interact very poorly. If one forgets about any electrostatic or intermolecular attractive forces between the molecules, one can assume that all collisions are perfectly elastic. One can visualize the gas as a collection of perfectly hard spheres which collide but ...
Removing the Mystery of Entropy and Thermodynamics – Part III
... temporal spreading function.11,12 The system’s time-averaged energy, E, is identified with the internal energy U, so S = S(U). Actually, because the allowed energies typically depend on the system volume, S = S(U, V). For the system plus an assumed constant temperature reservoir, the number of acces ...
... temporal spreading function.11,12 The system’s time-averaged energy, E, is identified with the internal energy U, so S = S(U). Actually, because the allowed energies typically depend on the system volume, S = S(U, V). For the system plus an assumed constant temperature reservoir, the number of acces ...
UNIT SUMMARIES 2014-2015 FUNDAMENTALS OF PHYSICS IN ENGINEERING I
... There are various types of bonds between atoms; however, in order to systematize their study two main types of bonds are considered: (a) ionic (formed between a metal and a non-metal) and (b) covalent (formed between non-metals). In practice, no substance forms totally ionic or totally covalent bond ...
... There are various types of bonds between atoms; however, in order to systematize their study two main types of bonds are considered: (a) ionic (formed between a metal and a non-metal) and (b) covalent (formed between non-metals). In practice, no substance forms totally ionic or totally covalent bond ...
The Ensembles
... which U, V and the number of particles N had to be constant. The appropriate thermodynamic function to describe the isolated system was the entropy, S = S(U, V, N ). Since the independent variables of S are constant for an isolated system, S itself must take a single, constant value at equilibrium a ...
... which U, V and the number of particles N had to be constant. The appropriate thermodynamic function to describe the isolated system was the entropy, S = S(U, V, N ). Since the independent variables of S are constant for an isolated system, S itself must take a single, constant value at equilibrium a ...
notes on thermodynamic formalism
... where now kB is Boltzmann’s constant, equal to approximately 1.38 × 10−23 m2 kg s−2 K−1 . We have not yet justified the existence of temperature as a state function taking numerical values; thus one may take Boyle’s law as the definition of temperature for an ideal gas. The internal energy of an ide ...
... where now kB is Boltzmann’s constant, equal to approximately 1.38 × 10−23 m2 kg s−2 K−1 . We have not yet justified the existence of temperature as a state function taking numerical values; thus one may take Boyle’s law as the definition of temperature for an ideal gas. The internal energy of an ide ...
Basic Thermodynamics - CERN Accelerator School
... increase”. The system changes in response to this tendency. Such a change is said to be ‘spontaneous’. If one imagines two possible macrostates for an isolated system, corresponding to two values of the number of possible microstates , the system will experimentally be found in the macrostate for ...
... increase”. The system changes in response to this tendency. Such a change is said to be ‘spontaneous’. If one imagines two possible macrostates for an isolated system, corresponding to two values of the number of possible microstates , the system will experimentally be found in the macrostate for ...
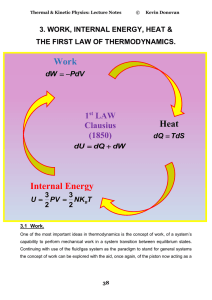
The First Law of Thermodynamics
... From the Kinetic theory, for monoatomic gases for biatomic gases ...
... From the Kinetic theory, for monoatomic gases for biatomic gases ...
Equipartition theorem

In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per degree of freedom in the translational motion of a molecule should equal that of its rotational motions.The equipartition theorem makes quantitative predictions. Like the virial theorem, it gives the total average kinetic and potential energies for a system at a given temperature, from which the system's heat capacity can be computed. However, equipartition also gives the average values of individual components of the energy, such as the kinetic energy of a particular particle or the potential energy of a single spring. For example, it predicts that every atom in a monatomic ideal gas has an average kinetic energy of (3/2)kBT in thermal equilibrium, where kB is the Boltzmann constant and T is the (thermodynamic) temperature. More generally, it can be applied to any classical system in thermal equilibrium, no matter how complicated. The equipartition theorem can be used to derive the ideal gas law, and the Dulong–Petit law for the specific heat capacities of solids. It can also be used to predict the properties of stars, even white dwarfs and neutron stars, since it holds even when relativistic effects are considered.Although the equipartition theorem makes very accurate predictions in certain conditions, it becomes inaccurate when quantum effects are significant, such as at low temperatures. When the thermal energy kBT is smaller than the quantum energy spacing in a particular degree of freedom, the average energy and heat capacity of this degree of freedom are less than the values predicted by equipartition. Such a degree of freedom is said to be ""frozen out"" when the thermal energy is much smaller than this spacing. For example, the heat capacity of a solid decreases at low temperatures as various types of motion become frozen out, rather than remaining constant as predicted by equipartition. Such decreases in heat capacity were among the first signs to physicists of the 19th century that classical physics was incorrect and that a new, more subtle, scientific model was required. Along with other evidence, equipartition's failure to model black-body radiation—also known as the ultraviolet catastrophe—led Max Planck to suggest that energy in the oscillators in an object, which emit light, were quantized, a revolutionary hypothesis that spurred the development of quantum mechanics and quantum field theory.