Here - Dorodnicyn Computing Centre of the Russian Academy of
... meta-mathematical version of the Reductio ad Absurdum (further - RAA) method, "proves" that the assumption is false. 3. First hidden necessary condition of Cantor's proof. - In the middle of the XX c., meta-mathematics announced Cantor's set theory "naive" [9] and soon the very mention of the term " ...
... meta-mathematical version of the Reductio ad Absurdum (further - RAA) method, "proves" that the assumption is false. 3. First hidden necessary condition of Cantor's proof. - In the middle of the XX c., meta-mathematics announced Cantor's set theory "naive" [9] and soon the very mention of the term " ...
Chapter 2.6 Notes: Prove Statements about Segments and Angles
... • A proof is a logical argument that shows a satement is true. Two-Column Proofs: • A two-column proof has numbered statements and corresponding reasons that show an argument in a logical order. • In a two-column proof, each statement in the lefthand column is either given information or the result ...
... • A proof is a logical argument that shows a satement is true. Two-Column Proofs: • A two-column proof has numbered statements and corresponding reasons that show an argument in a logical order. • In a two-column proof, each statement in the lefthand column is either given information or the result ...
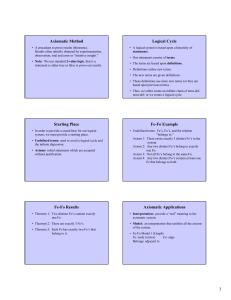
STEPS for INDIRECT PROOF - Fairfield Public Schools
... either because it CONTRADICTS one of these facts, or it leads to a statement that is ABSURD! (like above when we used the “GIVEN” angle measures to CONTRADICT the equilateral triangle theorem that states all angles of an equilateral triangle are congruent.) 3) Write a ‘therefore’ statement as a conc ...
... either because it CONTRADICTS one of these facts, or it leads to a statement that is ABSURD! (like above when we used the “GIVEN” angle measures to CONTRADICT the equilateral triangle theorem that states all angles of an equilateral triangle are congruent.) 3) Write a ‘therefore’ statement as a conc ...
Section 1.4 Mathematical Proofs
... Introduction A theorem1 is a proposition, deduced from given assumptions, and the chain of reasoning used to deduce the proposition is called a proof of the theorem. Theorems are ultimately based on a collection of principles considered so self-evident that their truth value is taken as fact. Such a ...
... Introduction A theorem1 is a proposition, deduced from given assumptions, and the chain of reasoning used to deduce the proposition is called a proof of the theorem. Theorems are ultimately based on a collection of principles considered so self-evident that their truth value is taken as fact. Such a ...
PREPOSITIONAL LOGIS
... • Logical inference creates new sentences that logically follow from a set of sentences (KB) • An inference rule is sound if every sentence X it produces when operating on a KB logically follows from the KB –i.e., inference rule creates no contradictions • An inference rule is complete if it can pro ...
... • Logical inference creates new sentences that logically follow from a set of sentences (KB) • An inference rule is sound if every sentence X it produces when operating on a KB logically follows from the KB –i.e., inference rule creates no contradictions • An inference rule is complete if it can pro ...
Incompleteness in a General Setting
... Much of the intricacy lies in the details of setting up and checking the properties of a coding system representing the syntax of an object language (typically, that of arithmetic) within that same language. These details are seldom illuminating and tend to obscure the core of the argument. For this ...
... Much of the intricacy lies in the details of setting up and checking the properties of a coding system representing the syntax of an object language (typically, that of arithmetic) within that same language. These details are seldom illuminating and tend to obscure the core of the argument. For this ...
CPS130, Lecture 1: Introduction to Algorithms
... 2001, some students who had already taken cps130 did not feel entirely comfortable with this material. To make the presentation more interesting, and perhaps a bit unique, I will do propositional logic and Boolean expressions together since they are really the same and their generalization to Boolea ...
... 2001, some students who had already taken cps130 did not feel entirely comfortable with this material. To make the presentation more interesting, and perhaps a bit unique, I will do propositional logic and Boolean expressions together since they are really the same and their generalization to Boolea ...
logica and critical thinking
... Self-defeating paradox: The concept of “all powerful” God Zeno’s paradox: An apparently unacceptable conclusion derived by apparently acceptable reasoning from apparently acceptable premises Semantic paradox: The liar’s paradox The lawyer’s paradox Prisoner’s dilemma Russell’s paradox (Barber’s para ...
... Self-defeating paradox: The concept of “all powerful” God Zeno’s paradox: An apparently unacceptable conclusion derived by apparently acceptable reasoning from apparently acceptable premises Semantic paradox: The liar’s paradox The lawyer’s paradox Prisoner’s dilemma Russell’s paradox (Barber’s para ...
MATHEMATICAL LOGIC CLASS NOTE 1. Propositional logic A
... (1) α is not satisfiable iff ¬α is tautology. (But a satisfiable sentence need not be tautology.) (2) α, β are tautologically equivalent iff α ↔ β is a tautology. (3) De Morgan’s law: ¬(φ ∧ ψ) ↔ ¬φ ∨ ¬ψ; ¬(φ ∨ ψ) ↔ ¬φ ∧ ¬ψ are both tautology. A literal is a sentence which is a sentence symbol, or the ...
... (1) α is not satisfiable iff ¬α is tautology. (But a satisfiable sentence need not be tautology.) (2) α, β are tautologically equivalent iff α ↔ β is a tautology. (3) De Morgan’s law: ¬(φ ∧ ψ) ↔ ¬φ ∨ ¬ψ; ¬(φ ∨ ψ) ↔ ¬φ ∧ ¬ψ are both tautology. A literal is a sentence which is a sentence symbol, or the ...
On Sets of Premises - Matematički Institut SANU
... ⊢ Gentzen writes → (which is more commonly used nowadays for the binary connective of implication; we use it below, as usual, for separating the sources and targets of arrows in categories), for A and B he uses Gothic letters, and for n and m Greek letters (see [6], Section I.2.3). The natural numbe ...
... ⊢ Gentzen writes → (which is more commonly used nowadays for the binary connective of implication; we use it below, as usual, for separating the sources and targets of arrows in categories), for A and B he uses Gothic letters, and for n and m Greek letters (see [6], Section I.2.3). The natural numbe ...
On the specification of sequent systems
... an involutive negation and this makes it difficult to address directly dualities in object-logic proof systems. This lack of dualities is particularly unfortunate when specifying sequent calculus [Gen69] since they play a central role in the theory of such proof systems. Pfenning in [Pfn95,Pfn00] us ...
... an involutive negation and this makes it difficult to address directly dualities in object-logic proof systems. This lack of dualities is particularly unfortunate when specifying sequent calculus [Gen69] since they play a central role in the theory of such proof systems. Pfenning in [Pfn95,Pfn00] us ...
A(x)
... Inference rules: MP (modus ponens), E (general quantifier elimination), I (existential quantifier insertion) Theorem: Proof: ...
... Inference rules: MP (modus ponens), E (general quantifier elimination), I (existential quantifier insertion) Theorem: Proof: ...
A(x)
... Inference rules: MP (modus ponens), E (general quantifier elimination), I (existential quantifier insertion) Theorem: Proof: ...
... Inference rules: MP (modus ponens), E (general quantifier elimination), I (existential quantifier insertion) Theorem: Proof: ...