Sequent calculus for predicate logic
... Lemma 3.2. A cut free derivation π of a sequent σ in either the classical or intuitionistic sequent calculus only contains Gentzen subformulas of formulas occurring in σ. But note that the definition of Gentzen subformula is such that ∀x P x has infinitely many Gentzen subformulas: indeed, each form ...
... Lemma 3.2. A cut free derivation π of a sequent σ in either the classical or intuitionistic sequent calculus only contains Gentzen subformulas of formulas occurring in σ. But note that the definition of Gentzen subformula is such that ∀x P x has infinitely many Gentzen subformulas: indeed, each form ...
1. Axioms and rules of inference for propositional logic. Suppose T
... 1. Axioms and rules of inference for propositional logic. Suppose T = (L, A, R) is a formal theory. Whenever H is a finite subset of L and C ∈ L it is evident that (H, C) ∈ R ⇒ H ` C. Fix a set X of propositional variables. We work with the language p(X). 1.1. The standard setup (or so I think). Thi ...
... 1. Axioms and rules of inference for propositional logic. Suppose T = (L, A, R) is a formal theory. Whenever H is a finite subset of L and C ∈ L it is evident that (H, C) ∈ R ⇒ H ` C. Fix a set X of propositional variables. We work with the language p(X). 1.1. The standard setup (or so I think). Thi ...
Truth and proof
... Tennant’s answer: Sound proof suffices for truth • Any proof in PA* of a sentence in the language of L, is a ground for asserting , even though might have no proof in the weaker system . All is needed, for the assertion of , is some proof of …In particular if it turns out that there is a pr ...
... Tennant’s answer: Sound proof suffices for truth • Any proof in PA* of a sentence in the language of L, is a ground for asserting , even though might have no proof in the weaker system . All is needed, for the assertion of , is some proof of …In particular if it turns out that there is a pr ...
pdf
... Story of Logic to motivate the ideas and ground them in a narrative that makes sense to every one interested in the subject. We also examine the subject that Hilbert called metamathematics where we use an informal mathematical theory to discuss properties of the object languages and logics we will s ...
... Story of Logic to motivate the ideas and ground them in a narrative that makes sense to every one interested in the subject. We also examine the subject that Hilbert called metamathematics where we use an informal mathematical theory to discuss properties of the object languages and logics we will s ...
A game semantics for proof search: Preliminary results - LIX
... which contains one constructor for each de Morgan pair of connectives in (linear) logic. Horn clauses are flat and represent only one “phase” in a computation: they support no alternation in polarities. In Section 4, we extend the language of neutral expressions to include a “switch” operator that s ...
... which contains one constructor for each de Morgan pair of connectives in (linear) logic. Horn clauses are flat and represent only one “phase” in a computation: they support no alternation in polarities. In Section 4, we extend the language of neutral expressions to include a “switch” operator that s ...
Label-free Modular Systems for Classical and Intuitionistic Modal
... both conjuncts are needed. With these five axioms one can, a priori, obtain 32 logics but some coincide, such that there are only 15, which can be arranged in a cube as shown in Figure 2. This cube has the same shape in the classical as well as in the intuitionistic setting. However, the two papers ...
... both conjuncts are needed. With these five axioms one can, a priori, obtain 32 logics but some coincide, such that there are only 15, which can be arranged in a cube as shown in Figure 2. This cube has the same shape in the classical as well as in the intuitionistic setting. However, the two papers ...
Label-free Modular Systems for Classical and Intuitionistic Modal
... both conjuncts are needed. With these five axioms one can, a priori, obtain 32 logics but some coincide, such that there are only 15, which can be arranged in a cube as shown in Figure 2. This cube has the same shape in the classical as well as in the intuitionistic setting. However, the two papers ...
... both conjuncts are needed. With these five axioms one can, a priori, obtain 32 logics but some coincide, such that there are only 15, which can be arranged in a cube as shown in Figure 2. This cube has the same shape in the classical as well as in the intuitionistic setting. However, the two papers ...
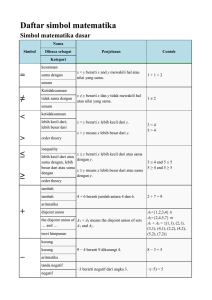
Daftar simbol matematika
... or join in a lattice or propositional logic, lattice theory exclusive or ...
... or join in a lattice or propositional logic, lattice theory exclusive or ...
Lesson 12
... 1. A, B are not formulas, but meta-symbols denoting any formula. Each axiom schema denotes an infinite class of formulas of a given form. If axioms were specified by concrete formulas, like 1. p (q p) 2. (p (q r)) ((p q) (p r)) 3. (q p) (p q) we would have to extend the set o ...
... 1. A, B are not formulas, but meta-symbols denoting any formula. Each axiom schema denotes an infinite class of formulas of a given form. If axioms were specified by concrete formulas, like 1. p (q p) 2. (p (q r)) ((p q) (p r)) 3. (q p) (p q) we would have to extend the set o ...
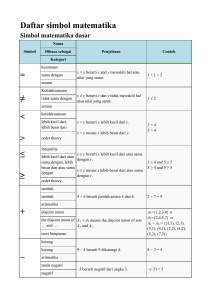
Daftar simbol matematika - Wikipedia bahasa Indonesia
... or join in a lattice or propositional logic, lattice theory exclusive or ...
... or join in a lattice or propositional logic, lattice theory exclusive or ...
Partial Grounded Fixpoints
... years. They showed that grounded fixpoints are an intuitive concept, closely related to exact (two-valued) stable fixpoints. In the context of logic programming, grounded fixpoints can be characterised using a generalised notion of unfounded set. Grounded fixpoints are lattice elements; in this work ...
... years. They showed that grounded fixpoints are an intuitive concept, closely related to exact (two-valued) stable fixpoints. In the context of logic programming, grounded fixpoints can be characterised using a generalised notion of unfounded set. Grounded fixpoints are lattice elements; in this work ...
Propositional Logic Syntax of Propositional Logic
... • Additional concepts (in addition to propositional logic) – complex objects • terms ...
... • Additional concepts (in addition to propositional logic) – complex objects • terms ...
The Foundations: Logic and Proofs - UTH e
... Solution: Let p denote “The diagnostic message is not stored in the buffer.” Let q denote “The diagnostic message is retransmitted” The specification can be written as: p ∨ q, p→ q, ¬p. When p is false and q is true all three statements are true. So the specification is consistent. What if “The di ...
... Solution: Let p denote “The diagnostic message is not stored in the buffer.” Let q denote “The diagnostic message is retransmitted” The specification can be written as: p ∨ q, p→ q, ¬p. When p is false and q is true all three statements are true. So the specification is consistent. What if “The di ...