Lecture 34 Notes
... Mike then goes on to note that the function rule essentially leads to Russell’s paradox. He gives the “Russell” version (p.17). Next Mike shows that Musser’s attempted fix also fails. That was for the programming language Euclid. He comments that in our book, A Programming Logic, 1978, we use a tota ...
... Mike then goes on to note that the function rule essentially leads to Russell’s paradox. He gives the “Russell” version (p.17). Next Mike shows that Musser’s attempted fix also fails. That was for the programming language Euclid. He comments that in our book, A Programming Logic, 1978, we use a tota ...
Propositional Logic Predicate Logic
... “There exists x s.t. A” B is true for some individual x. We also use individual constant a, b, c, etc. For some specific theories, we may write ∀x ∈ X.A or ∃x ∈ X.A to specify the set that x ranges over. Note. Nullary predicates (or, predicates with zero variables) are propositions. ...
... “There exists x s.t. A” B is true for some individual x. We also use individual constant a, b, c, etc. For some specific theories, we may write ∀x ∈ X.A or ∃x ∈ X.A to specify the set that x ranges over. Note. Nullary predicates (or, predicates with zero variables) are propositions. ...
Homework 5
... (3) Construct an example of a formula that is satisfiable in a denumerable universe but not in any finite one (exercise 3, page 50 of Smullyan). (4) Show that a first-order formula A is valid if and only if ∼A is satisfiable. Show that A is satisfiable if and only if ∼A is valid (exercise 4, page 50 ...
... (3) Construct an example of a formula that is satisfiable in a denumerable universe but not in any finite one (exercise 3, page 50 of Smullyan). (4) Show that a first-order formula A is valid if and only if ∼A is satisfiable. Show that A is satisfiable if and only if ∼A is valid (exercise 4, page 50 ...
What is Logic?
... Completeness(週延): Is every tautology a theorem? Decidability(可推導): Does an algorithm exist that will determine if a wff is valid? Monotonicity(不受破壞): Can a valid logical proof be made invalid by adding additional premises or assumptions? ...
... Completeness(週延): Is every tautology a theorem? Decidability(可推導): Does an algorithm exist that will determine if a wff is valid? Monotonicity(不受破壞): Can a valid logical proof be made invalid by adding additional premises or assumptions? ...
Negative translation - Homepages of UvA/FNWI staff
... obtained from intuitionistic logic by adding an additional axiom (for instance, the Law of Excluded Middle ϕ ∨ ¬ϕ). However, the opposite point of view makes sense as well: one could also think of intuitionistic logic as an extension of classical logic. The reason for this is that there is a faithfu ...
... obtained from intuitionistic logic by adding an additional axiom (for instance, the Law of Excluded Middle ϕ ∨ ¬ϕ). However, the opposite point of view makes sense as well: one could also think of intuitionistic logic as an extension of classical logic. The reason for this is that there is a faithfu ...
Chapter 7 Propositional and Predicate Logic
... Completeness(週延): Is every tautology a theorem? Decidability(可推導): Does an algorithm exist that will determine if a wff is valid? Monotonicity(不受破壞): Can a valid logical proof be made invalid by adding additional premises or assumptions? ...
... Completeness(週延): Is every tautology a theorem? Decidability(可推導): Does an algorithm exist that will determine if a wff is valid? Monotonicity(不受破壞): Can a valid logical proof be made invalid by adding additional premises or assumptions? ...
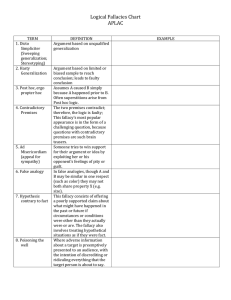
Logical Fallacies Chart APLAC TERM DEFINITION EXAMPLE 1
... This fallacy's most popular appearance is in the form of a challenging question, because questions with contradictory premises are such brain teasers. Someone tries to win support for their argument or idea by exploiting her or his opponent's feelings of pity or guilt. In false analogies, though A a ...
... This fallacy's most popular appearance is in the form of a challenging question, because questions with contradictory premises are such brain teasers. Someone tries to win support for their argument or idea by exploiting her or his opponent's feelings of pity or guilt. In false analogies, though A a ...
powerpoint - IDA.LiU.se
... be used each time a line is added to the proof The selected entailment rules are called the inference rules of this particular inference system ...
... be used each time a line is added to the proof The selected entailment rules are called the inference rules of this particular inference system ...
Normalised and Cut-free Logic of Proofs
... From a Gentzen-style point of view, we can formulate two similar sequent calculi for the two systems Lp and Ilp, respectively (see Artemov [2002]). Although simple and cut-free, these sequent calculi fail to satisfy certain properties that are standardly required from a “good" sequent calculus (in P ...
... From a Gentzen-style point of view, we can formulate two similar sequent calculi for the two systems Lp and Ilp, respectively (see Artemov [2002]). Although simple and cut-free, these sequent calculi fail to satisfy certain properties that are standardly required from a “good" sequent calculus (in P ...
Assignment 6
... (c) Define x < y to mean ∃z.(z 6= 0 & y = x + z), prove ∀x. ∃y.(x < y) and show the evidence term. (2) If we apply the minimization operator to a function f (x, y) that is always positive at x, e.g. ∀y. f (x, y) 6= 0, then it does not produce a value but “diverges,” on some input x. The domain of su ...
... (c) Define x < y to mean ∃z.(z 6= 0 & y = x + z), prove ∀x. ∃y.(x < y) and show the evidence term. (2) If we apply the minimization operator to a function f (x, y) that is always positive at x, e.g. ∀y. f (x, y) 6= 0, then it does not produce a value but “diverges,” on some input x. The domain of su ...
The Origin of Proof Theory and its Evolution
... Hilbert's ε-calculus is based on an extension of the language of predicate logic by a termforming operator εx. This operator is governed by the critical axiom A(t)⊃A(εx A(x)), where t is an arbitrary term. Within the ε-calculus quantifiers become definable by xA(x) A(εxA(x)) and ∀x A(x) A(εx¬A(x)) T ...
... Hilbert's ε-calculus is based on an extension of the language of predicate logic by a termforming operator εx. This operator is governed by the critical axiom A(t)⊃A(εx A(x)), where t is an arbitrary term. Within the ε-calculus quantifiers become definable by xA(x) A(εxA(x)) and ∀x A(x) A(εx¬A(x)) T ...
Friedman`s Translation
... Theorem 1.5. If ` A is derivable in classical predicate logic and if no free variable of R occurs in the derivation, then ` A¬R is derivable in intuitionistic predicate logic. In order to obtain Theorem 1.5 for arithmetic, it remains to show that HA∗ proves the ¬R -translation of all its axioms. The ...
... Theorem 1.5. If ` A is derivable in classical predicate logic and if no free variable of R occurs in the derivation, then ` A¬R is derivable in intuitionistic predicate logic. In order to obtain Theorem 1.5 for arithmetic, it remains to show that HA∗ proves the ¬R -translation of all its axioms. The ...
Why Does the Failure to Differentiate Reason from
... you looked again they were there again, but what makes you think they had been there in the interval?” You would only be able to say “because I see them whenever I look.” The sceptic would say “then you ought to infer that they are caused by your looking.” You will never succeed in getting any evide ...
... you looked again they were there again, but what makes you think they had been there in the interval?” You would only be able to say “because I see them whenever I look.” The sceptic would say “then you ought to infer that they are caused by your looking.” You will never succeed in getting any evide ...
ppt
... statements are true, what other statements can you also deduce are true? • If I tell you that all men are mortal, and Socrates is a man, what can you deduce? ...
... statements are true, what other statements can you also deduce are true? • If I tell you that all men are mortal, and Socrates is a man, what can you deduce? ...
coppin chapter 07e
... Soundness: Is every theorem valid? Completeness: Is every tautology a theorem? Decidability: Does an algorithm exist that will determine if a wff is valid? Monotonicity: Can a valid logical proof be made invalid by adding additional premises or assumptions? ...
... Soundness: Is every theorem valid? Completeness: Is every tautology a theorem? Decidability: Does an algorithm exist that will determine if a wff is valid? Monotonicity: Can a valid logical proof be made invalid by adding additional premises or assumptions? ...
Section 6.1 How Do We Reason? We make arguments, where an
... The hope is that we make valid arguments, where an argument is valid if the truth of the premises implies the truth of the conclusion. We can use rules of logic to make valid arguments. The most common rule of logic is modus ponens (mode that affirms). If A and B be are statements and “if A then B” ...
... The hope is that we make valid arguments, where an argument is valid if the truth of the premises implies the truth of the conclusion. We can use rules of logic to make valid arguments. The most common rule of logic is modus ponens (mode that affirms). If A and B be are statements and “if A then B” ...
Programming and Problem Solving with Java: Chapter 14
... Soundness: Is every theorem valid? Completeness: Is every tautology a theorem? Decidability: Does an algorithm exist that will determine if a wff is valid? Monotonicity: Can a valid logical proof be made invalid by adding additional premises or assumptions? ...
... Soundness: Is every theorem valid? Completeness: Is every tautology a theorem? Decidability: Does an algorithm exist that will determine if a wff is valid? Monotonicity: Can a valid logical proof be made invalid by adding additional premises or assumptions? ...
Title PI name/institution
... Joseph Wang (UCSD) and Evgeny Katz (Clarkson University) Project Objectives: To develop next-generation ‘sense and treat’ autonomous devices for enhancing the survival rate among A) injured soldiers in the battlefield. B) ...
... Joseph Wang (UCSD) and Evgeny Katz (Clarkson University) Project Objectives: To develop next-generation ‘sense and treat’ autonomous devices for enhancing the survival rate among A) injured soldiers in the battlefield. B) ...
pdf
... 2. For the completeness proof of refinement logic we have introduced the following rules. H ` A ∨ (B ∨ C) by orAssocL H ` (A⊃B) ∨ G∗ by impR∗ H ` (A ∨ B) ∨ C H, A ` B ∨ G∗ Prove that both rules can be derived in refinement logic, i.e. give a proof fragment that simultates the rules. 3. Prove that th ...
... 2. For the completeness proof of refinement logic we have introduced the following rules. H ` A ∨ (B ∨ C) by orAssocL H ` (A⊃B) ∨ G∗ by impR∗ H ` (A ∨ B) ∨ C H, A ` B ∨ G∗ Prove that both rules can be derived in refinement logic, i.e. give a proof fragment that simultates the rules. 3. Prove that th ...
PHILOSOPHY 326 / MATHEMATICS 307 SYMBOLIC LOGIC This
... proofs in a system of natural deduction for the logic of propositions. This course does not have a fixed and predetermined syllabus. There is core content which will be covered in class, and a number of options for additional content. The specific content of the course, the type and frequency of exa ...
... proofs in a system of natural deduction for the logic of propositions. This course does not have a fixed and predetermined syllabus. There is core content which will be covered in class, and a number of options for additional content. The specific content of the course, the type and frequency of exa ...
pdf
... Church and Turing in 1936 laid the foundations for computer science by defining equivalent notions of computability – Church for software, Turing for hardware. Their ideas were used to make precise the insights of Brouwer from 1900 that mathematics is based on fundamental human intuitions about numb ...
... Church and Turing in 1936 laid the foundations for computer science by defining equivalent notions of computability – Church for software, Turing for hardware. Their ideas were used to make precise the insights of Brouwer from 1900 that mathematics is based on fundamental human intuitions about numb ...
IntroToLogic - Department of Computer Science
... The validity of first order logic is not decidable. (It is semi-decidable.) If a theorem is logically entailed by an axiom, you can prove that it is. But if it is not, you can’t necessarily prove that it is not. (You may go on infinitely with your ...
... The validity of first order logic is not decidable. (It is semi-decidable.) If a theorem is logically entailed by an axiom, you can prove that it is. But if it is not, you can’t necessarily prove that it is not. (You may go on infinitely with your ...
Logic: the `Art of Thinking`
... bad) incorrect reasoning’,4 or ‘the study of consistent sets of beliefs’,5 or ‘like ethics, logic can also be called a normative science. How must I think in order to reach the goal, truth?’,6 or ‘a central goal of logic is to study logical truth and logical consequence.’7 From Aristotle’s Pri ...
... bad) incorrect reasoning’,4 or ‘the study of consistent sets of beliefs’,5 or ‘like ethics, logic can also be called a normative science. How must I think in order to reach the goal, truth?’,6 or ‘a central goal of logic is to study logical truth and logical consequence.’7 From Aristotle’s Pri ...