Exam-Computational_Logic-Subjects_2016
... 1. Using a proof method: a) semantic method (truth table, semantic tableau, conjunctive normal form) b) syntactic method (resolution, definition of deduction, the theorem of deduction and its reverse) c) direct method (truth table, conjunctive normal form, definition of deduction, the theorem of ded ...
... 1. Using a proof method: a) semantic method (truth table, semantic tableau, conjunctive normal form) b) syntactic method (resolution, definition of deduction, the theorem of deduction and its reverse) c) direct method (truth table, conjunctive normal form, definition of deduction, the theorem of ded ...
PDF
... Let FO(Σ) be a first order language over signature Σ. Recall that the axioms for FO(Σ) are (universal) generalizations of wff’s belonging to one of the following six schemas: 1. A → (B → A) 2. (A → (B → C)) → ((A → B) → (A → C)) 3. ¬¬A → A 4. ∀x(A → B) → (∀xA → ∀xB), where x ∈ V 5. A → ∀xA, where x ...
... Let FO(Σ) be a first order language over signature Σ. Recall that the axioms for FO(Σ) are (universal) generalizations of wff’s belonging to one of the following six schemas: 1. A → (B → A) 2. (A → (B → C)) → ((A → B) → (A → C)) 3. ¬¬A → A 4. ∀x(A → B) → (∀xA → ∀xB), where x ∈ V 5. A → ∀xA, where x ...
3409 - educatepk.com
... Note: All questions carry equal marks. Q. 1 Design an excess-3-to-BCD code converter using a 4-bit full-adders MSI circuit. ...
... Note: All questions carry equal marks. Q. 1 Design an excess-3-to-BCD code converter using a 4-bit full-adders MSI circuit. ...
The origin of the technical use of "sound argument": a postscript
... original). (By a deductive argument he means one "in which the truth of the premises guarantees (or is intended to guarantee) the truth of the conclusion without appeal to other reasons" (35-36).) The idea that a deductively valid argument with true premisses is a good argument appears in the textbo ...
... original). (By a deductive argument he means one "in which the truth of the premises guarantees (or is intended to guarantee) the truth of the conclusion without appeal to other reasons" (35-36).) The idea that a deductively valid argument with true premisses is a good argument appears in the textbo ...
Logic: Introduction - Department of information engineering and
... Modern Logic teaches us that one claim is a logical consequence of another if there is no way the latter could be true without the former also being true. It is also used to disconfirm a theory if a particular claim is a logical consequence of a theory, and we discover that the claim is false, then ...
... Modern Logic teaches us that one claim is a logical consequence of another if there is no way the latter could be true without the former also being true. It is also used to disconfirm a theory if a particular claim is a logical consequence of a theory, and we discover that the claim is false, then ...
Definition - Rogelio Davila
... A traditional way of characterizing validity and logical consequence is in terms of derivation, or proof, and inference rules. This may be accomplished either by an axiomatic system or, through a natural deduction system. Some definitions: Def. An axiom is a statement considered as valid. Def. An in ...
... A traditional way of characterizing validity and logical consequence is in terms of derivation, or proof, and inference rules. This may be accomplished either by an axiomatic system or, through a natural deduction system. Some definitions: Def. An axiom is a statement considered as valid. Def. An in ...
Artificial Intelligence
... validity of arguments. we are not concerned with the truth of statements, but rather with their validity. • That is to say, although the following argument is clearly logical, it is not something that we would consider to be true: All lemons are blue Mary is a lemon Therefore, Mary is blue ...
... validity of arguments. we are not concerned with the truth of statements, but rather with their validity. • That is to say, although the following argument is clearly logical, it is not something that we would consider to be true: All lemons are blue Mary is a lemon Therefore, Mary is blue ...
To What Type of Logic Does the "Tetralemma" Belong?
... affairs, without taking a position on whether that event or state of affairs actually obtains. For example, let A be the proposition “It rained all day yesterday”. In itself, A tells us nothing about yesterday’s weather; it only raises an implicit question. But if we then either deny or affirm A, we ans ...
... affairs, without taking a position on whether that event or state of affairs actually obtains. For example, let A be the proposition “It rained all day yesterday”. In itself, A tells us nothing about yesterday’s weather; it only raises an implicit question. But if we then either deny or affirm A, we ans ...
characterization of prime numbers by
... Thus, x → y differs from x → y in that x → y does not always take the k designated value n − 1 when x < y and if x = y then x → y = n − 1 only when x ∈ {0, 1, n − 1}. Logic Kn is defined in analogy with Ln , and Kn is the set of all matrix functions from Kn . To prove the theorems the following two ...
... Thus, x → y differs from x → y in that x → y does not always take the k designated value n − 1 when x < y and if x = y then x → y = n − 1 only when x ∈ {0, 1, n − 1}. Logic Kn is defined in analogy with Ln , and Kn is the set of all matrix functions from Kn . To prove the theorems the following two ...
valid - Informatik Uni Leipzig
... Let us consider the following axiom schemata: T: 2ϕ → ϕ (knowledge axiom) 4: 2ϕ → 22ϕ (positive introspection) 5: 3ϕ → 23ϕ (negative introspection: equivalently ¬2ϕ → 2¬2ϕ) B: ϕ → 23ϕ D: 2ϕ → 3ϕ (disbelief in the negation, equivalently 2ϕ → ¬2¬ϕ) . . . and the following classes of frames, for which ...
... Let us consider the following axiom schemata: T: 2ϕ → ϕ (knowledge axiom) 4: 2ϕ → 22ϕ (positive introspection) 5: 3ϕ → 23ϕ (negative introspection: equivalently ¬2ϕ → 2¬2ϕ) B: ϕ → 23ϕ D: 2ϕ → 3ϕ (disbelief in the negation, equivalently 2ϕ → ¬2¬ϕ) . . . and the following classes of frames, for which ...
first order logic
... Ideally, we can come up with a “perfect” logical system, which is consistent (not having contradictions) and is powerful (can derive everything that is true). But Gödel proved that there is no perfect logical system. This is called the Gödel’s incompleteness theorem. It is an important and surprisin ...
... Ideally, we can come up with a “perfect” logical system, which is consistent (not having contradictions) and is powerful (can derive everything that is true). But Gödel proved that there is no perfect logical system. This is called the Gödel’s incompleteness theorem. It is an important and surprisin ...
The Notion of Formal Logic
... tion. Second intentions are relations which are formed by the mind through comparison of objects and which, therefore, have their foundations in first intentions—in known objects: «relationes quae attribuuntur ab intel lectu rebus intellectis, prout sunt intellectae», as St. Thomas explains2. Since ...
... tion. Second intentions are relations which are formed by the mind through comparison of objects and which, therefore, have their foundations in first intentions—in known objects: «relationes quae attribuuntur ab intel lectu rebus intellectis, prout sunt intellectae», as St. Thomas explains2. Since ...
Notes
... Intuitionistic logic is the basis of constructive mathematics. Constructive mathematics takes a much more conservative view of truth than classical mathematics. It is concerned less with truth than with provability. Its main proponents were Kronecker and Brouwer around the beginning of the last cent ...
... Intuitionistic logic is the basis of constructive mathematics. Constructive mathematics takes a much more conservative view of truth than classical mathematics. It is concerned less with truth than with provability. Its main proponents were Kronecker and Brouwer around the beginning of the last cent ...
CLASSICAL LOGIC and FUZZY LOGIC
... Another example comes from ancient Greece. Does the liar from Crete lie when he claims, ‘‘All Cretians are liars?’’ If he is telling the truth, his statement is false. But if his statement is false, he is not telling the truth. A simpler form of this paradox is the two-word proposition, ‘‘I lie.’’ T ...
... Another example comes from ancient Greece. Does the liar from Crete lie when he claims, ‘‘All Cretians are liars?’’ If he is telling the truth, his statement is false. But if his statement is false, he is not telling the truth. A simpler form of this paradox is the two-word proposition, ‘‘I lie.’’ T ...
Predicate Logic
... – It is sunny : SUNNY – It is windy : WINDY – It is raining then it is not sunny (This is logical ...
... – It is sunny : SUNNY – It is windy : WINDY – It is raining then it is not sunny (This is logical ...
Logic, deontic. The study of principles of reasoning pertaining to
... prohibition, moral commitment and other normative matters. Although often described as a branch of logic, deontic logic lacks the "topic-neutrality" characteristic of logic proper. It is better viewed as an application of logic to ethical concepts, in much the same way as formal geometry is an appli ...
... prohibition, moral commitment and other normative matters. Although often described as a branch of logic, deontic logic lacks the "topic-neutrality" characteristic of logic proper. It is better viewed as an application of logic to ethical concepts, in much the same way as formal geometry is an appli ...
1
... i. 2P ⊃ P ii. P ⊃ 23P iii. 2P ⊃ 3P Moreover, if one of the formulas φ is not valid on frame (Wi , Ri ), give a world w in Wi and a forcing relation ` between Wi and {P } such that w ` ¬φ. (c) Show that P →23P is valid on a Kripke Frame if and only if the accessibility relation is symmetric. (Hint; f ...
... i. 2P ⊃ P ii. P ⊃ 23P iii. 2P ⊃ 3P Moreover, if one of the formulas φ is not valid on frame (Wi , Ri ), give a world w in Wi and a forcing relation ` between Wi and {P } such that w ` ¬φ. (c) Show that P →23P is valid on a Kripke Frame if and only if the accessibility relation is symmetric. (Hint; f ...
Full version - Villanova Computer Science
... They can be divided into two major classes: Hilbert-style and Gentzen-style. Hilbert-style systems are axiom-based while Gentzen-style systems are rule-based. Gentzen-style systems have a number of advantages, including existence of straightforward proof search algorithms. In this course we will dea ...
... They can be divided into two major classes: Hilbert-style and Gentzen-style. Hilbert-style systems are axiom-based while Gentzen-style systems are rule-based. Gentzen-style systems have a number of advantages, including existence of straightforward proof search algorithms. In this course we will dea ...
Lecture 16 Notes
... We will look briefly at the incompleteness result since that has received a good deal of attention as a contrast to the Gödel completeness result for classical FOL. The folklore has it that Gödel’s result cannot be constructive.1 We will not explore Kripke models and the important result of Vim Ve ...
... We will look briefly at the incompleteness result since that has received a good deal of attention as a contrast to the Gödel completeness result for classical FOL. The folklore has it that Gödel’s result cannot be constructive.1 We will not explore Kripke models and the important result of Vim Ve ...
Philosophy 120 Symbolic Logic I H. Hamner Hill
... soundness • In 1931 Kurt Gödel proved that it is impossible to have a formal system that is both complete and sound! This discovery changed the nature of mathematics forever. • Gödel’s result ended the constructivist project and ended the quest for certainty in mathematics. • Gödel’s result was one ...
... soundness • In 1931 Kurt Gödel proved that it is impossible to have a formal system that is both complete and sound! This discovery changed the nature of mathematics forever. • Gödel’s result ended the constructivist project and ended the quest for certainty in mathematics. • Gödel’s result was one ...
Logic - Mathematical Institute SANU
... A close relative of the word deduction is proof, when it refers to a correct deduction where the premises are true, or acceptable in some sense. A more distant relative is argument, because an argument may, but need not, be deductive. The study of argumentation in general belongs more to rhetoric th ...
... A close relative of the word deduction is proof, when it refers to a correct deduction where the premises are true, or acceptable in some sense. A more distant relative is argument, because an argument may, but need not, be deductive. The study of argumentation in general belongs more to rhetoric th ...
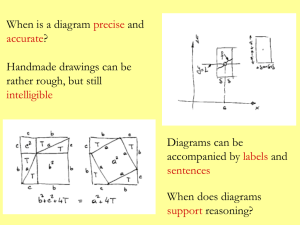
Diagrams in logic and mathematics - CFCUL
... “the laws of logic are not sculpted in stone, eternal and immutable. A realistic look at the development of mathematics shows that the reasons for a theorem are found only after digging deep and focusing upon the possibility of a theorem. The discovery of such hidden reasons is the work of the mathe ...
... “the laws of logic are not sculpted in stone, eternal and immutable. A realistic look at the development of mathematics shows that the reasons for a theorem are found only after digging deep and focusing upon the possibility of a theorem. The discovery of such hidden reasons is the work of the mathe ...