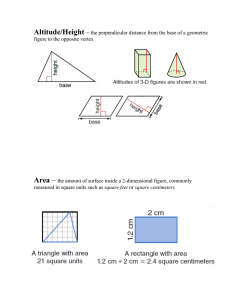
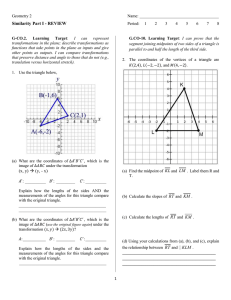
First Semester Geometry Exam Review – January 2015 Chapter 1
... Alternate Interior Angles________________________________________________________+ Same Side Interior Angles________________________________________________________ ...
... Alternate Interior Angles________________________________________________________+ Same Side Interior Angles________________________________________________________ ...
Lines and planes
... (they’re the same plane) or they don’t intersect at all. If two planes are not parallel then they intersect at a line. The equation of their line of intersection can be solved by finding Point on line: to do this, solve the linear equations of the planes simultaneously. Direction: this must be p ...
... (they’re the same plane) or they don’t intersect at all. If two planes are not parallel then they intersect at a line. The equation of their line of intersection can be solved by finding Point on line: to do this, solve the linear equations of the planes simultaneously. Direction: this must be p ...
Unit 4_Final_Vocab_Exam_Rev_Ans_13
... an expression is to replace the expression with an equivalent expression having as few terms as possible or a numeral if possible. 12. A(n) equation or inequality indicating the relationship between two mathematical mathematical ...
... an expression is to replace the expression with an equivalent expression having as few terms as possible or a numeral if possible. 12. A(n) equation or inequality indicating the relationship between two mathematical mathematical ...
8th Math Unit 1 - Fairfield Township School
... sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. 8.G.3: Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates. 8.G.4: Understand that a t ...
... sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. 8.G.3: Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates. 8.G.4: Understand that a t ...
Geometry Syllabus 2016-2017
... Use the relationships between angles formed by two lines cut by a transversal to a) determine whether two lines are parallel; b) verify the parallelism, using algebraic and coordinate methods as well as deductive proofs; and c) solve real-world problems involving angles formed when parallel lines ...
... Use the relationships between angles formed by two lines cut by a transversal to a) determine whether two lines are parallel; b) verify the parallelism, using algebraic and coordinate methods as well as deductive proofs; and c) solve real-world problems involving angles formed when parallel lines ...
TTUISD Geometry 1A First Semester Guide and Practice Exam
... Use the SAS, SSS, AAS, ASA, and HL Postulates and Theorems of Congruence Use the Base Angles Theorem Use properties of and construct isosceles and equilateral triangles Use congruent triangles and prove constructions Place figures in the coordinate plane Write coordinate proofs Special S ...
... Use the SAS, SSS, AAS, ASA, and HL Postulates and Theorems of Congruence Use the Base Angles Theorem Use properties of and construct isosceles and equilateral triangles Use congruent triangles and prove constructions Place figures in the coordinate plane Write coordinate proofs Special S ...
Rational Number
... quantity. When we make a mathematics equation out of an ordinary statement by using a variable(s), it makes the thinking process mechanized and automatic, thus making the solution process much easier. ...
... quantity. When we make a mathematics equation out of an ordinary statement by using a variable(s), it makes the thinking process mechanized and automatic, thus making the solution process much easier. ...
MYP 9 Extended Review Sheets
... A helicopter hovers directly above the landing pad on the roof of a 125-m high building. A person is standing 145 m from the base of the building. The angle of elevation of the helicopter from this person is 58. Assume the landing pad is at the edge of the roof closest to the person on the ground. ...
... A helicopter hovers directly above the landing pad on the roof of a 125-m high building. A person is standing 145 m from the base of the building. The angle of elevation of the helicopter from this person is 58. Assume the landing pad is at the edge of the roof closest to the person on the ground. ...
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.