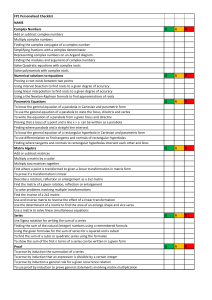
Lecture 14 – More damned mathematics
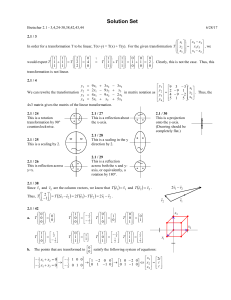
... Matrix form • [x’; y’] = [ cosΘ sin Θ; -sinΘ cos Θ] ×[ x; y] • where “ ; ” indicates new row, column elements separated by spaces ...
... Matrix form • [x’; y’] = [ cosΘ sin Θ; -sinΘ cos Θ] ×[ x; y] • where “ ; ” indicates new row, column elements separated by spaces ...
Hw #2 pg 109 1-13odd, pg 101 23,25,27,29
... We can multiply the vector x to CA = CAx = x which can be rewritten as CAx = x because x was being multiplied by an identity matrix. Since Ax= 0 we can substitute that in x = CAx and get C0 = 0 which shows that it has only the trivial solution. This also shows us that A is linearly independent becau ...
... We can multiply the vector x to CA = CAx = x which can be rewritten as CAx = x because x was being multiplied by an identity matrix. Since Ax= 0 we can substitute that in x = CAx and get C0 = 0 which shows that it has only the trivial solution. This also shows us that A is linearly independent becau ...
SVDslides.ppt
... • If I observe the outputs of a linear system and watch what is coming, could I figure out what the inputs were? • Related problem: If you start with 2 things in the input space and run them through the system and compare the outputs, can we still distinguish them as different? • So when is the line ...
... • If I observe the outputs of a linear system and watch what is coming, could I figure out what the inputs were? • Related problem: If you start with 2 things in the input space and run them through the system and compare the outputs, can we still distinguish them as different? • So when is the line ...
Problem Set 2
... (this is the sort of thing that occurs for a spin-1/2 system subjected to a magnetic field in the x-direction). • Find the eigenvectors and eigenvalues of H. What are the possible energies that can occur in this quantum system? • If the system starts out at time t = 0 in the state ...
... (this is the sort of thing that occurs for a spin-1/2 system subjected to a magnetic field in the x-direction). • Find the eigenvectors and eigenvalues of H. What are the possible energies that can occur in this quantum system? • If the system starts out at time t = 0 in the state ...
DSP_Test1_2006
... components, Y = [Y[0], Y[1], …, Y[N1]]T (where T is the matrix transpose). We can represent the forward transform as Y = Wx, where W is an NN matrix. Similarly, we can also represent the inverse transform as x = AY, where A is an NN matrix. Question: Please write down the NN matrices W and A. (b ...
... components, Y = [Y[0], Y[1], …, Y[N1]]T (where T is the matrix transpose). We can represent the forward transform as Y = Wx, where W is an NN matrix. Similarly, we can also represent the inverse transform as x = AY, where A is an NN matrix. Question: Please write down the NN matrices W and A. (b ...
A recursive parameterisation of unitary matrices
... Hence these vectors represent two parameters, for example ...
... Hence these vectors represent two parameters, for example ...