Chapter 1 Linear Equations and Graphs
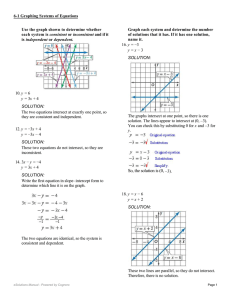
... and C are constants (A and B not both 0), and x and y are variables. A solution of an equation in two variables is an ordered pair of real numbers that satisfy the equation. For example, (4,3) is a solution of 3x - 2y = 6. The solution set of an equation in two variables is the set of all soluti ...
... and C are constants (A and B not both 0), and x and y are variables. A solution of an equation in two variables is an ordered pair of real numbers that satisfy the equation. For example, (4,3) is a solution of 3x - 2y = 6. The solution set of an equation in two variables is the set of all soluti ...
Electromagnetic waves in vacuum.
... Polarization of EM waves The two classes of solutions (Ex,By) and (Ey,Bx) are independent: they represent the two polarization modes of EM radiation. As the E and B fields lie on a plane, these modes correspond to linear polarizations. A generic (unpolarized) EM wave is a superposition of the two m ...
... Polarization of EM waves The two classes of solutions (Ex,By) and (Ey,Bx) are independent: they represent the two polarization modes of EM radiation. As the E and B fields lie on a plane, these modes correspond to linear polarizations. A generic (unpolarized) EM wave is a superposition of the two m ...