Lab2
... Type the following to plot the level curves of the potential function on the left side: ...
... Type the following to plot the level curves of the potential function on the left side: ...
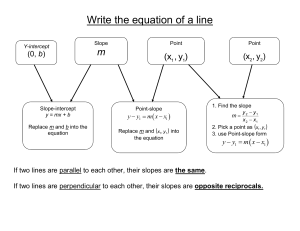
Key Concepts for Day 54 Quiz 1 on System of Linear Equations
... Key Concepts for Day 54 Quiz 1 on System of Linear Equations: System of Linear Equations Two or more equations in the same variable form To solve a system of two equations with two variables, you must We have learned three methods for solving a system of linear equations, they are The three possible ...
... Key Concepts for Day 54 Quiz 1 on System of Linear Equations: System of Linear Equations Two or more equations in the same variable form To solve a system of two equations with two variables, you must We have learned three methods for solving a system of linear equations, they are The three possible ...
MAT282 * Differential Equations
... From a numerical standpoint it is sometimes useful to rewrite an equation as a system This procedure is pretty simple but requires some care The general idea is to, in a system of order n (so the highest derivative is y (n)), write all of the lower derivatives as new (unknown) functions and set it u ...
... From a numerical standpoint it is sometimes useful to rewrite an equation as a system This procedure is pretty simple but requires some care The general idea is to, in a system of order n (so the highest derivative is y (n)), write all of the lower derivatives as new (unknown) functions and set it u ...
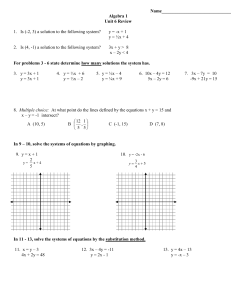
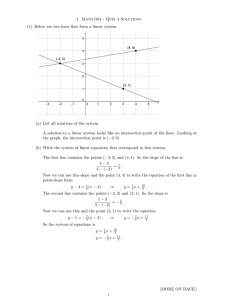
Lesson 1: 2 Equations 2 Unknowns
... Note 1: Systems of Equations Systems of equations involve two or more variables related to each other through a set of equations. The solution to the system is the set of values of the variables which satisfies all equations. Algebraic methods used to solve are: Elimination Substitution ...
... Note 1: Systems of Equations Systems of equations involve two or more variables related to each other through a set of equations. The solution to the system is the set of values of the variables which satisfies all equations. Algebraic methods used to solve are: Elimination Substitution ...
x + 1
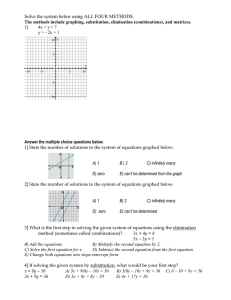
... For problems 27 – 29, state whether the equation has one solution, no solutions, or if it is an Identity (Infinitely Many Solutions) 27. 4(x – 3) = 4x – 12 ...
... For problems 27 – 29, state whether the equation has one solution, no solutions, or if it is an Identity (Infinitely Many Solutions) 27. 4(x – 3) = 4x – 12 ...