Lagrangian Dynamics
... If a system is made up of n particles, we can specify the positions of all particles with 3n coordinates. On the other hand, if there are m equations of constraints (for example, if some particles were connected to form rigid bodies), then the 3n coordinates are not all independent. There will be on ...
... If a system is made up of n particles, we can specify the positions of all particles with 3n coordinates. On the other hand, if there are m equations of constraints (for example, if some particles were connected to form rigid bodies), then the 3n coordinates are not all independent. There will be on ...
Graphing and Writing Equations of Lines PowerPoint
... Forms of Linear Equations O There are three main forms for the equation ...
... Forms of Linear Equations O There are three main forms for the equation ...
Reply to: "Comments on `A generic length
... The goal of Umlauf and Burchard (2003) was to formulate a model for a quantity c } k ml n that exhibits controllable properties and is mathematically and numerically optimal under certain constraints essential for turbulent oceanic ows. In general, these constraints can lead to exponents m and n b ...
... The goal of Umlauf and Burchard (2003) was to formulate a model for a quantity c } k ml n that exhibits controllable properties and is mathematically and numerically optimal under certain constraints essential for turbulent oceanic ows. In general, these constraints can lead to exponents m and n b ...
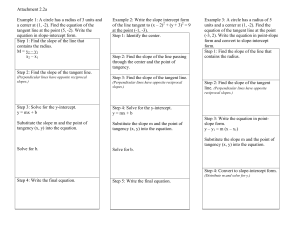
Class Notes - Math.utah.edu
... These notes were prepared for the University of Utah’s Math 1010 refresher course. They asssume that the user has had the Math 1010 course Intermediate Algebra or its equivalent (in high school or college). The notes work like this: in order to help you focus on the areas where you need the most imp ...
... These notes were prepared for the University of Utah’s Math 1010 refresher course. They asssume that the user has had the Math 1010 course Intermediate Algebra or its equivalent (in high school or college). The notes work like this: in order to help you focus on the areas where you need the most imp ...