On the use of fuzzy stable models for inconsistent classical logic
... then every finite normal program P defined over L has at least a stable model. Proof: The idea is to apply Brouwer’s fix-point theorem. Specifically, we show that the operator assigning each interpretation I the interpretation R(I) = lfp(TPI ) is continuous. Note that this operator can be seen as a ...
... then every finite normal program P defined over L has at least a stable model. Proof: The idea is to apply Brouwer’s fix-point theorem. Specifically, we show that the operator assigning each interpretation I the interpretation R(I) = lfp(TPI ) is continuous. Note that this operator can be seen as a ...
Variables In Real Life: A Jar Of Spare Change
... century before the first computers were actually developed. ...
... century before the first computers were actually developed. ...
duality of quantifiers ¬8xA(x) 9x¬A(x) ¬9xA(x) 8x¬A(x)
... There are problems that cannot be solved by computer programs (i.e. algorithms) even assuming unlimited time and space. What is an “algorithm”? The following are all equivalent: - C programs, scheme programs, Java programs . . . - Turing machines (Turing’s idea of an “algorithm”) ...
... There are problems that cannot be solved by computer programs (i.e. algorithms) even assuming unlimited time and space. What is an “algorithm”? The following are all equivalent: - C programs, scheme programs, Java programs . . . - Turing machines (Turing’s idea of an “algorithm”) ...
Using Modal Logics to Express and Check Global Graph Properties
... tested with a specific method that usually does not generalize to other different problems or properties. A logical framework, on the other hand, may provide this level of generalization. In an intuitive and non-technical language, this can be stated as follows. Consider a logic L with its formulas ...
... tested with a specific method that usually does not generalize to other different problems or properties. A logical framework, on the other hand, may provide this level of generalization. In an intuitive and non-technical language, this can be stated as follows. Consider a logic L with its formulas ...
Soundness and completeness
... contrapositive in three steps. What the Model Existence Lemma states and how that statement is used in the completeness proof. What consistent and maximally consistent sets are. That every consistent set is contained in a maximally consistent set and why. That the proof of the MEL works basically by ...
... contrapositive in three steps. What the Model Existence Lemma states and how that statement is used in the completeness proof. What consistent and maximally consistent sets are. That every consistent set is contained in a maximally consistent set and why. That the proof of the MEL works basically by ...
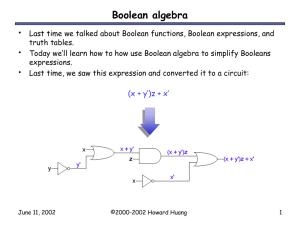
Boolean Algebra
... We can build complex functions from just the basic Boolean values “true” and “false,” and the operations AND, OR and NOT. Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expr ...
... We can build complex functions from just the basic Boolean values “true” and “false,” and the operations AND, OR and NOT. Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expr ...
10 pp. - Department of Computer Science
... Terms Tm are built from variables and (certain, see Section 1.5 of [9] for details) constants by λ-abstraction and application. We represent the latter as concatenation and we agree that it is left-associative in order to avoid excessive parenthesizing. All variables and constants have an a priori f ...
... Terms Tm are built from variables and (certain, see Section 1.5 of [9] for details) constants by λ-abstraction and application. We represent the latter as concatenation and we agree that it is left-associative in order to avoid excessive parenthesizing. All variables and constants have an a priori f ...
(pdf)
... We can give the meanings that we intended for the languages to have by simply interpreting the symbols as what we would expect them to mean. For instance you could define an LGroup -structure by (Z, +, 0) where + is the conventional addition. Note also though that (N, +, 0) is an LGroup -structure, ...
... We can give the meanings that we intended for the languages to have by simply interpreting the symbols as what we would expect them to mean. For instance you could define an LGroup -structure by (Z, +, 0) where + is the conventional addition. Note also though that (N, +, 0) is an LGroup -structure, ...
CHAPTER 1. SENTENTIAL LOGIC 1. Introduction In sentential logic
... • If 7 is not odd then 2 is odd • If 7 is odd and 2 is odd then 2 is not prime • (7 is odd and 2 is odd) or 2 is prime We have improved on English in the last example by using parentheses to resolve an ambiguity. And, or, not, if . . . then (or implies) are called (sentential) connectives. Using the ...
... • If 7 is not odd then 2 is odd • If 7 is odd and 2 is odd then 2 is not prime • (7 is odd and 2 is odd) or 2 is prime We have improved on English in the last example by using parentheses to resolve an ambiguity. And, or, not, if . . . then (or implies) are called (sentential) connectives. Using the ...
Witness and Counterexample Automata for ACTL
... counterexamples [4] or proof-like counterexamples [10], on the other side establishing the subsets of the logics whose formulae guarantee linear computation paths as counterexamples which completely explain the failure [1, 12]. Our work in this field has been motivated by another trend that has cons ...
... counterexamples [4] or proof-like counterexamples [10], on the other side establishing the subsets of the logics whose formulae guarantee linear computation paths as counterexamples which completely explain the failure [1, 12]. Our work in this field has been motivated by another trend that has cons ...
Simple multiplicative proof nets with units
... Here is a passage from Girard’s Proof Nets: the Parallel Syntax for Proof Theory [Gir96, §A.2]1 : There are two multiplicative neutrals, 1 and ⊥, and two rules, the axiom ⊢ 1 and the weakening rule: from ⊢ Γ, deduce ⊢ Γ, ⊥. Both rules are handled by means of links with one conclusion and no premise; ...
... Here is a passage from Girard’s Proof Nets: the Parallel Syntax for Proof Theory [Gir96, §A.2]1 : There are two multiplicative neutrals, 1 and ⊥, and two rules, the axiom ⊢ 1 and the weakening rule: from ⊢ Γ, deduce ⊢ Γ, ⊥. Both rules are handled by means of links with one conclusion and no premise; ...
Hilbert Type Deductive System for Sentential Logic, Completeness
... Proof: The following is a proof of α→α α→[(α→α)→α], {α→[(α→α)→ α]}→{[α→(α→α)]→(α→α)], (α→(α→α))→(α→α), α→(α→α), α→α The first wff is an instance of Axiom (i), the second––of Axiom (ii), the third is inferred from the first two via modus ponens, the fourth is an instance of Axiom (i) and the fifth i ...
... Proof: The following is a proof of α→α α→[(α→α)→α], {α→[(α→α)→ α]}→{[α→(α→α)]→(α→α)], (α→(α→α))→(α→α), α→(α→α), α→α The first wff is an instance of Axiom (i), the second––of Axiom (ii), the third is inferred from the first two via modus ponens, the fourth is an instance of Axiom (i) and the fifth i ...
Three Solutions to the Knower Paradox
... by one of the rules of inferences. One of the possible interpretations of Gödel famous theorem deals with this notion of proof: if a formal system satisfies certain conditions, there exists a formula p such that neither p nor ¬p is formally provable in that system. But in Myhill’s opinion (see [12]) ...
... by one of the rules of inferences. One of the possible interpretations of Gödel famous theorem deals with this notion of proof: if a formal system satisfies certain conditions, there exists a formula p such that neither p nor ¬p is formally provable in that system. But in Myhill’s opinion (see [12]) ...
On the Complexity of Resolution-based Proof Systems
... Note that the first set of clauses forces every pigeon to fly to some hole and the second ensures that no hole will be doubly occupied. Therefore, refuting these clauses, that is, proving that they are contradictory, would prove the principle true. Observe that the principle is not expressed by the ...
... Note that the first set of clauses forces every pigeon to fly to some hole and the second ensures that no hole will be doubly occupied. Therefore, refuting these clauses, that is, proving that they are contradictory, would prove the principle true. Observe that the principle is not expressed by the ...
FIRST ORDER QUANTIFIERS IN MONADIC SECOND ORDER
... graphs, ∆n+2 6⊆ F OB(Σn ), F O(Σn ) ∩ F O(Πn ) 6⊆ B(Σn ), and F O(Σn+1 ) ∩ F O(Πn+1 ) 6⊆ F OB(Σn ), where F O denotes the positive first order closure, and F OB denotes the first order/Boolean closure. Ajtai, Fagin, and Stockmeyer in [AFS98] and [AFS00] proposed closed monadic NP, in which first ord ...
... graphs, ∆n+2 6⊆ F OB(Σn ), F O(Σn ) ∩ F O(Πn ) 6⊆ B(Σn ), and F O(Σn+1 ) ∩ F O(Πn+1 ) 6⊆ F OB(Σn ), where F O denotes the positive first order closure, and F OB denotes the first order/Boolean closure. Ajtai, Fagin, and Stockmeyer in [AFS98] and [AFS00] proposed closed monadic NP, in which first ord ...
Remarks on Second-Order Consequence
... only that each informally proven theorem be provable by means of the calculus (in other words, when formalizing, we do not mean to be true to proofs, but to theorems). As soon as we state this demand we see the difficulty it involves, for if the notion of an informal theorem turned out to be open-en ...
... only that each informally proven theorem be provable by means of the calculus (in other words, when formalizing, we do not mean to be true to proofs, but to theorems). As soon as we state this demand we see the difficulty it involves, for if the notion of an informal theorem turned out to be open-en ...
Insights into Modal Slash Logic and Modal Decidability
... position (~ab,~i, χ); note that the rule in no way utilizes the independence indication. If ψ = ∀xχ, player A selects an element b ∈ M . Finally, if ψ is (negated) atomic, E wins and A loses if ψ is satisfied in M by the variable assignment induced by the tuple ~a, else the players receive the rever ...
... position (~ab,~i, χ); note that the rule in no way utilizes the independence indication. If ψ = ∀xχ, player A selects an element b ∈ M . Finally, if ψ is (negated) atomic, E wins and A loses if ψ is satisfied in M by the variable assignment induced by the tuple ~a, else the players receive the rever ...