Task 3 - The Wise Man and the Chess Board
... c) 6y³ 4y 1.5 y2 6. Illustrate these results, which show the oscillation of a weight on a spring, on a graph. Put time on the horizontal axis ( use 1 cm = 1 second) and displacement on the vertical axis (use 1 cm = a displacement of 1 cm). ...
... c) 6y³ 4y 1.5 y2 6. Illustrate these results, which show the oscillation of a weight on a spring, on a graph. Put time on the horizontal axis ( use 1 cm = 1 second) and displacement on the vertical axis (use 1 cm = a displacement of 1 cm). ...
Chapter 1 Mid Chapter Review Math 7
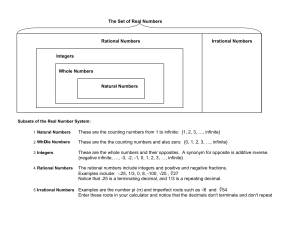
... 1. When adding or subtracting decimals you line up the ____. 2. A value of a number whose distance is calculated by how far it is from zero on a number line. 3. What type of numbers are easy to compute mentally ...
... 1. When adding or subtracting decimals you line up the ____. 2. A value of a number whose distance is calculated by how far it is from zero on a number line. 3. What type of numbers are easy to compute mentally ...
Op-Amp Imperfections in The Linear Range of Operations Gain and
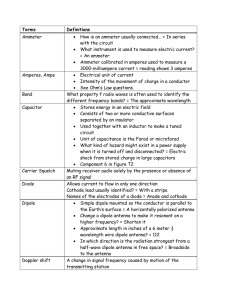
... Op-Amp Imperfections in The Linear Range of Operations Gain and Bandwidth Limitations Ideal op amps have infinite open-loop gain magnitude (AoL is infinite), but the gain of a real op amp is finite and a function of frequency dc open-circuit differential voltage gain is typically between 104 to ...
... Op-Amp Imperfections in The Linear Range of Operations Gain and Bandwidth Limitations Ideal op amps have infinite open-loop gain magnitude (AoL is infinite), but the gain of a real op amp is finite and a function of frequency dc open-circuit differential voltage gain is typically between 104 to ...
Full text
... which has initial terms uQ = 0 and u1 = 1. Difference equations of the form (2) are expressible in a matrix form analogous to (1). This formulation is unfortunately absent in some general works on difference equations (e.g. [2], [4]), although it has been used extensively by Bernstein (e.g. [1]) and ...
... which has initial terms uQ = 0 and u1 = 1. Difference equations of the form (2) are expressible in a matrix form analogous to (1). This formulation is unfortunately absent in some general works on difference equations (e.g. [2], [4]), although it has been used extensively by Bernstein (e.g. [1]) and ...
Mathematics of radio engineering

The mathematics of radio engineering is the mathematical description by complex analysis of the electromagnetic theory applied to radio. Waves have been studied since ancient times and many different techniques have developed of which the most useful idea is the superposition principle which apply to radio waves. The Huygen's principle, which says that each wavefront creates an infinite number of new wavefronts that can be added, is the base for this analysis.