“We cannot hold a torch to light another`s path without brightening
... The product of zero & a number is zero. ...
... The product of zero & a number is zero. ...
St Pius X Numeracy Evening
... After lots of visual, practical and mental subtraction work with single digit numbers including use of a number line and use of relevant language such as difference between, minus, how many less is?... how many less than?..., subtract, take, take away etc. children learn to subtract larger numbers. ...
... After lots of visual, practical and mental subtraction work with single digit numbers including use of a number line and use of relevant language such as difference between, minus, how many less is?... how many less than?..., subtract, take, take away etc. children learn to subtract larger numbers. ...
Study Guide - East Lyme Public Schools
... Estimation by rounding to the highest place value, or rounding to 10, 100, or 1000. 2 by 2, 3 by 1 or 3by 2-digit multiplication with or without decimals. You can use traditional, expanded or array method. When asked to use a model, use array or place value (dot) methods. With decimals, multiply as ...
... Estimation by rounding to the highest place value, or rounding to 10, 100, or 1000. 2 by 2, 3 by 1 or 3by 2-digit multiplication with or without decimals. You can use traditional, expanded or array method. When asked to use a model, use array or place value (dot) methods. With decimals, multiply as ...
LO: To calculate angles on a straight line and use a protractor to
... List six parts of the body that only have 3 letters. Mathematical Activity Complete the following listing the known fact, and the adjusted answer. E.g. 20 x 3 – Known fact is 2 x3 = 6 Adjusted answer is 60 because 20 is 10 time bigger than 2. a) 40 x 3 b) 6 x 50 c) 50 x 4 d) 80 x 2 e) 7 x 40 Use the ...
... List six parts of the body that only have 3 letters. Mathematical Activity Complete the following listing the known fact, and the adjusted answer. E.g. 20 x 3 – Known fact is 2 x3 = 6 Adjusted answer is 60 because 20 is 10 time bigger than 2. a) 40 x 3 b) 6 x 50 c) 50 x 4 d) 80 x 2 e) 7 x 40 Use the ...
R1 Real Numbers
... specified final digit in the decimal. Rounding Identify the specified final digit in the decimal. If the next digit is 5 or more, add 1 to the final digit. Otherwise leave the number as it appears. ...
... specified final digit in the decimal. Rounding Identify the specified final digit in the decimal. If the next digit is 5 or more, add 1 to the final digit. Otherwise leave the number as it appears. ...
Whole Number Operations and Their Properties
... Commutative Property of Addition and Multiplication Addition and Multiplication are commutative: switching the order of two numbers being added or multiplied does not change the result. When adding numbers, it doesn't matter which number comes first, the sum will be the same. Another way to look at ...
... Commutative Property of Addition and Multiplication Addition and Multiplication are commutative: switching the order of two numbers being added or multiplied does not change the result. When adding numbers, it doesn't matter which number comes first, the sum will be the same. Another way to look at ...
Microsoft Word version
... Thank you for the opportunity to provide the enrichment program. We hope your students enjoyed it as much as we did. The topics we covered with your students, including the activities used, are checked off below: TOPICS COVERED 1. Number Patterns and Explanations □ Examples of patterns in number seq ...
... Thank you for the opportunity to provide the enrichment program. We hope your students enjoyed it as much as we did. The topics we covered with your students, including the activities used, are checked off below: TOPICS COVERED 1. Number Patterns and Explanations □ Examples of patterns in number seq ...
Physical Science 20 Notes Unit 1 Part 1B
... Examples on board When multiplying numbers expressed in scientific notation, the exponents of powers of 10 are added even if they are not the same. You multiply the numbers preceding the powers of 10 and then add the exponents to get the product. For example (4.3 x 104)(6.2 x 105) = 26.7 x 109. This ...
... Examples on board When multiplying numbers expressed in scientific notation, the exponents of powers of 10 are added even if they are not the same. You multiply the numbers preceding the powers of 10 and then add the exponents to get the product. For example (4.3 x 104)(6.2 x 105) = 26.7 x 109. This ...
ADDITION In Years 2 and 3, children use two main methods of
... Staff use these as guidance, so you will be supporting your child in the same ways. All children learn at different paces. Some will be using strategies from lower in school, and others will progress to the next ones. This booklet is provided as a guide only, but if you would like a copy of the year ...
... Staff use these as guidance, so you will be supporting your child in the same ways. All children learn at different paces. Some will be using strategies from lower in school, and others will progress to the next ones. This booklet is provided as a guide only, but if you would like a copy of the year ...
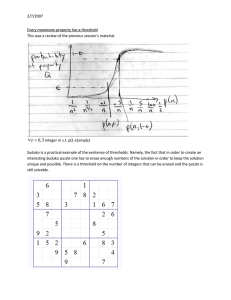
Threshold in N(n,p)
... We are interested in the threshold for when there is an arithmetic progression of length k. Where the arithmetic progression looks as: a, a+b, a+2b, a+3b; all of which are elements of the progression set. Let Xk be the number of arithmetic progressions of length k: E(Xk)=n2pk This is justified by th ...
... We are interested in the threshold for when there is an arithmetic progression of length k. Where the arithmetic progression looks as: a, a+b, a+2b, a+3b; all of which are elements of the progression set. Let Xk be the number of arithmetic progressions of length k: E(Xk)=n2pk This is justified by th ...
Dino and Jessica were doing their homework when Dino got to a
... Algebra 2/Trigonometry Unit 2 Quiz REVIEW ...
... Algebra 2/Trigonometry Unit 2 Quiz REVIEW ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.