PHƯƠNG PHÁP PHÁT HIỆN CÁC ĐỊNH LÍ MỚI VỀ HÌNH HỌC
... Given 6 vertices ABCDEF inscribed in a circle and d is an arbitrary line. Let Oab be the point of intersection of mid-perpendicular AB and d. Let (Oab ) be the circle with its center Oab and its radius Oab A . Similarly to the circles (Ode ), (Obc ), (Oef ), (Oaf ), (Odc ). Let X , X '; Y , Y '; Z , ...
... Given 6 vertices ABCDEF inscribed in a circle and d is an arbitrary line. Let Oab be the point of intersection of mid-perpendicular AB and d. Let (Oab ) be the circle with its center Oab and its radius Oab A . Similarly to the circles (Ode ), (Obc ), (Oef ), (Oaf ), (Odc ). Let X , X '; Y , Y '; Z , ...
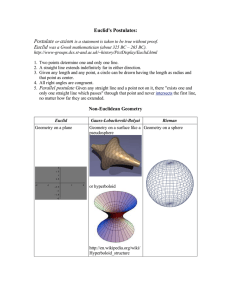
Postulates - mrsemmensmath
... Consider OB and a point A on one side of OB . The rays of the form OA can be matched one to one with the real numbers from ...
... Consider OB and a point A on one side of OB . The rays of the form OA can be matched one to one with the real numbers from ...