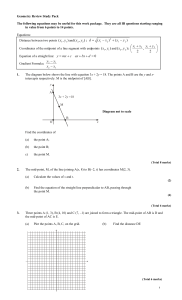
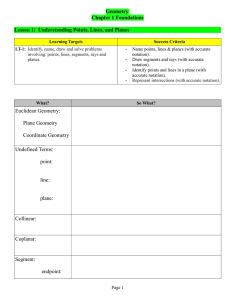
Section 9.1- Basic Notions
... 2. If two points lie in a plane, then the line containing the points lies in the plane. 3. If two distinct planes intersect, then their intersection is a line. 4. There is exactly one plane that contains any three distinct noncollinear points. 5. A line and a point not on the line determine a plane. ...
... 2. If two points lie in a plane, then the line containing the points lies in the plane. 3. If two distinct planes intersect, then their intersection is a line. 4. There is exactly one plane that contains any three distinct noncollinear points. 5. A line and a point not on the line determine a plane. ...