$doc.title
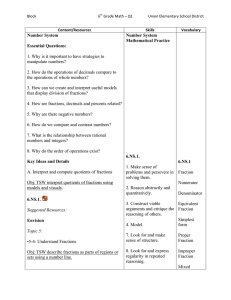
... 1. How can we create and interpret useful models that display division of fractions? 2. How are fractions, decimals and percents related? A. Division of fractions can be solved using a variety of methods. Equivalent quantities are shown using fractions, decimals and percents. 6.NS.1. Obj: TSW covert ...
... 1. How can we create and interpret useful models that display division of fractions? 2. How are fractions, decimals and percents related? A. Division of fractions can be solved using a variety of methods. Equivalent quantities are shown using fractions, decimals and percents. 6.NS.1. Obj: TSW covert ...
Logical Inference and Mathematical Proof
... Lemma: less important theorem used to prove other theorems. Corollary: theorem that trivially follows another theorem. ...
... Lemma: less important theorem used to prove other theorems. Corollary: theorem that trivially follows another theorem. ...
32(2)
... m = 3: The assertion P3 ID /}; P2 is equivalent to x3 DX;XJ. m = 4; Note that x4 = aif^, x = d^, and x3 = i^. Therefore, applying concatenation to the alignments cdz)d;c and P4 ZDP2;P3 implies that x4 IDX;CX3. Consequently, by Lemma 1,(1) cannot hold for m = 4, since x2 begins with a rf. Similar rea ...
... m = 3: The assertion P3 ID /}; P2 is equivalent to x3 DX;XJ. m = 4; Note that x4 = aif^, x = d^, and x3 = i^. Therefore, applying concatenation to the alignments cdz)d;c and P4 ZDP2;P3 implies that x4 IDX;CX3. Consequently, by Lemma 1,(1) cannot hold for m = 4, since x2 begins with a rf. Similar rea ...
Discrete Mathematics
... CCCC. No group can be all zeroes. a) How many SSNs are available? If nothing was un-allowed, there would be 109 . Then we can figure out how many of each un-allowed case there are. 8.7) I have 30 photos to post on my website. I’m planning to post these on two web pages, one marked “Friends” and the ...
... CCCC. No group can be all zeroes. a) How many SSNs are available? If nothing was un-allowed, there would be 109 . Then we can figure out how many of each un-allowed case there are. 8.7) I have 30 photos to post on my website. I’m planning to post these on two web pages, one marked “Friends” and the ...
CST Review Questions
... Divide the number of miles by the amount of time it took to get home to find his speed from LA to his house. Compare this speed with that provided in the question Determine the solution, based on the ...
... Divide the number of miles by the amount of time it took to get home to find his speed from LA to his house. Compare this speed with that provided in the question Determine the solution, based on the ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.