DOC
... These notes serve as course notes for an undergraduate course in number theory. Most if not all universities worldwide offer introductory courses in number theory for math majors and in many cases as an elective course. The notes contain a useful introduction to important topics that need to be addr ...
... These notes serve as course notes for an undergraduate course in number theory. Most if not all universities worldwide offer introductory courses in number theory for math majors and in many cases as an elective course. The notes contain a useful introduction to important topics that need to be addr ...
![[1] presented a deter](http://s1.studyres.com/store/data/014924405_1-eae03e3c4df5f7c19074d5b588e63597-300x300.png)
lecture3.1 - Computer and Information Sciences
... 4. Inverse : there exists an element a-1 for every a in G, such that a.a-1 = a-1.a = e ...
... 4. Inverse : there exists an element a-1 for every a in G, such that a.a-1 = a-1.a = e ...
An explicit version of Birch`s Theorem
... sufficiently many variables in terms of the number and degrees of these polynomials. While bounds have been obtained for the number of variables which suffice to guarantee the existence of a non-trivial zero, in all but the simplest cases such bounds as are available are too weak to have warranted e ...
... sufficiently many variables in terms of the number and degrees of these polynomials. While bounds have been obtained for the number of variables which suffice to guarantee the existence of a non-trivial zero, in all but the simplest cases such bounds as are available are too weak to have warranted e ...
Chapter 9 Section 1
... Polynomial: The sum of one or more monomials is called a polynomial. Monomial: A monomial is a number, a variable, or a product of numbers and variables that have only positive exponents. Binomial: A polynomial with two terms is a binomial. Trinomial: A polynomial with three terms is a trinomial. ...
... Polynomial: The sum of one or more monomials is called a polynomial. Monomial: A monomial is a number, a variable, or a product of numbers and variables that have only positive exponents. Binomial: A polynomial with two terms is a binomial. Trinomial: A polynomial with three terms is a trinomial. ...
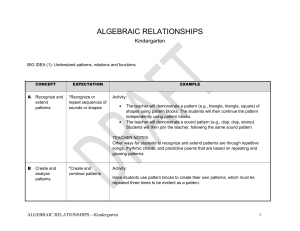
Algebraic Relationships
... “Through classroom discussions of different representations during the pre-K–2 years, students should develop an increased ability to use the symbols as a means of recording their thinking. In the earliest years, teachers may provide scaffolding for students by writing for them until they have the a ...
... “Through classroom discussions of different representations during the pre-K–2 years, students should develop an increased ability to use the symbols as a means of recording their thinking. In the earliest years, teachers may provide scaffolding for students by writing for them until they have the a ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.