Prime-perfect numbers - Dartmouth Math Home
... Our upper-bound proof covers a class of numbers somewhat wider than that of the primeperfects. Let rad(n) denote the largest squarefree divisor of n, so that n is prime-perfect if and only if rad(n) = rad(σ(n)). Call n prime-abundant if every prime dividing n divides σ(n), i.e., if rad(n) | rad(σ(n) ...
... Our upper-bound proof covers a class of numbers somewhat wider than that of the primeperfects. Let rad(n) denote the largest squarefree divisor of n, so that n is prime-perfect if and only if rad(n) = rad(σ(n)). Call n prime-abundant if every prime dividing n divides σ(n), i.e., if rad(n) | rad(σ(n) ...
presentation source - Personal Home Pages (at UEL)
... 5 mm wide cannot say the area is 5 because the units are not defined Change one of the lengths to have same prefix e.g. 1 m = 103 mm so area is 5 x 103 mm2 or 5 mm = 5 x 10-3 m so area is 5 x 10-3 m2 ...
... 5 mm wide cannot say the area is 5 because the units are not defined Change one of the lengths to have same prefix e.g. 1 m = 103 mm so area is 5 x 103 mm2 or 5 mm = 5 x 10-3 m so area is 5 x 10-3 m2 ...
Year 8 - Portland Place School
... contexts and describe the general term in simple cases. 1.4 Express simple functions in words, then using symbols; represent them in mappings. 1.5 Use letter symbols to represent unknown numbers or variables. 1.6 Identify the necessary information to understand or simplify a context or problem; repr ...
... contexts and describe the general term in simple cases. 1.4 Express simple functions in words, then using symbols; represent them in mappings. 1.5 Use letter symbols to represent unknown numbers or variables. 1.6 Identify the necessary information to understand or simplify a context or problem; repr ...
36(4)
... Since Fn mdFn+l are coprime integers, and because any prime/? divides infinitely many Fibonacci numbers Fn_l = Fn+l-Fn, for every prime p the congruence Fn = Fn+l # 0 modp is satisfied for infinitely many pairs of Fibonacci numbers Fn and Fn+l. Proof of Theorem 1.2: Let 36 c: (0,1) be the subset of ...
... Since Fn mdFn+l are coprime integers, and because any prime/? divides infinitely many Fibonacci numbers Fn_l = Fn+l-Fn, for every prime p the congruence Fn = Fn+l # 0 modp is satisfied for infinitely many pairs of Fibonacci numbers Fn and Fn+l. Proof of Theorem 1.2: Let 36 c: (0,1) be the subset of ...
statement
... between 5 and 10. The program will then output the number typed in by the user. However, the program should make sure that the number typed in is indeed between 5 and 10. Repeat the previous exercise except that the user is limited to three (3) trials only. If the user exceeds this limit, the progra ...
... between 5 and 10. The program will then output the number typed in by the user. However, the program should make sure that the number typed in is indeed between 5 and 10. Repeat the previous exercise except that the user is limited to three (3) trials only. If the user exceeds this limit, the progra ...
LORENTZIAN PYTHAGOREAN TRIPLES and LORENTZIAN UNIT CIRCLE
... a Lorentzian primitive Pyhtagorean triple. So d must equal to 1 or 2. But d also divides (b − c) (b + c) = a2 , and a is odd, so d must be 1. In other words, the only number dividing both b − c and b + c is 1, so b − c and b + c have no common factor. It is known that the product is a square since ( ...
... a Lorentzian primitive Pyhtagorean triple. So d must equal to 1 or 2. But d also divides (b − c) (b + c) = a2 , and a is odd, so d must be 1. In other words, the only number dividing both b − c and b + c is 1, so b − c and b + c have no common factor. It is known that the product is a square since ( ...
Algebra Recall 2
... basis. He was paid $50.00 a week, so he decided to start by saving 5c the first week, 10c the next week, 20c the third week, continuing to double the amount he saved each week. He was shocked to find that, by the 11th week, he could not afford to keep up his plan. (a) Copy the following table and co ...
... basis. He was paid $50.00 a week, so he decided to start by saving 5c the first week, 10c the next week, 20c the third week, continuing to double the amount he saved each week. He was shocked to find that, by the 11th week, he could not afford to keep up his plan. (a) Copy the following table and co ...
Finding Slope – Intercept Form From Points
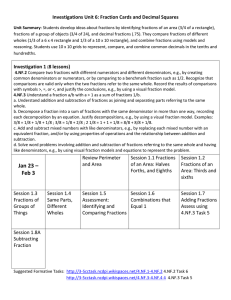
... both positive. x2 + 10x + 25 = (x + 5)(x + 5) If b is negative and c is positive, then the factors you will use are both negative. x2 – 5x + 6 = (x -2)(x – 3) If b is negative and c is negative, then one factor will be positive and the other will be negative. The negative number must have a larg ...
... both positive. x2 + 10x + 25 = (x + 5)(x + 5) If b is negative and c is positive, then the factors you will use are both negative. x2 – 5x + 6 = (x -2)(x – 3) If b is negative and c is negative, then one factor will be positive and the other will be negative. The negative number must have a larg ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.