Powerpoint 1
... Why must a given measurement always be reported to the correct number of significant figures? The significant figures in a calculated answer often depend on the number of significant figures of the measurements used in the calculation. How does the precision of a calculated answer compare to the pre ...
... Why must a given measurement always be reported to the correct number of significant figures? The significant figures in a calculated answer often depend on the number of significant figures of the measurements used in the calculation. How does the precision of a calculated answer compare to the pre ...
Fractions PowerPoint Tutorial
... The top number (numerator) stands for the number of shaded pieces The bottom number (denominator) stands for number of pieces in 1 whole…in this case four Therefore here we have 4/4 or 1 whole pizza pie ...
... The top number (numerator) stands for the number of shaded pieces The bottom number (denominator) stands for number of pieces in 1 whole…in this case four Therefore here we have 4/4 or 1 whole pizza pie ...
Strong Normality of Numbers - CECM
... The number 1/3 has the binary representation 0.010101 . . .. Since the digits 0 and 1 occur equally frequently, this number is simply normal in the base 2. One wants to exclude such repeating patterns. A number is normal to the base r if every t-string in its base r expansion occurs with a frequency ...
... The number 1/3 has the binary representation 0.010101 . . .. Since the digits 0 and 1 occur equally frequently, this number is simply normal in the base 2. One wants to exclude such repeating patterns. A number is normal to the base r if every t-string in its base r expansion occurs with a frequency ...
Prime Factorization
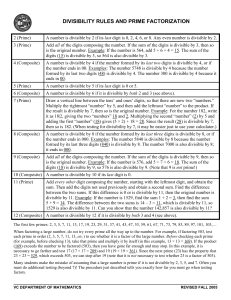
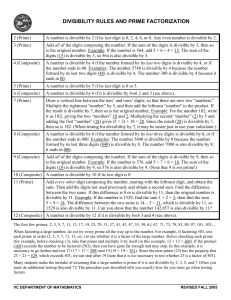
... are both prime, you are finished. If either is not prime, then rewrite it as the product of smaller natural numbers. Continue until all the factors are prime. ...
... are both prime, you are finished. If either is not prime, then rewrite it as the product of smaller natural numbers. Continue until all the factors are prime. ...
sig fig - stcscience6
... 1. Significant figures are used for measured numbers and for numbers derived from measurements; does not include definitions (ex. 1000ml=1L) or counting numbers (ex. 1,2,3 etc) 10 mm = 1cm = (2 significant figures) 100cm = 1m = (3 significant figures) 1000g = 1kg= (4 significant digits) ...
... 1. Significant figures are used for measured numbers and for numbers derived from measurements; does not include definitions (ex. 1000ml=1L) or counting numbers (ex. 1,2,3 etc) 10 mm = 1cm = (2 significant figures) 100cm = 1m = (3 significant figures) 1000g = 1kg= (4 significant digits) ...
Part 1: Introduction
... In both complement methods - positive numbers represented as in the signed-magnitude method A negative number -Y is represented by R-Y where R is a constant This representation satisfies -(-Y )=Y since R-(R-Y)=Y ECE666/Koren Part.1 .18 ...
... In both complement methods - positive numbers represented as in the signed-magnitude method A negative number -Y is represented by R-Y where R is a constant This representation satisfies -(-Y )=Y since R-(R-Y)=Y ECE666/Koren Part.1 .18 ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.