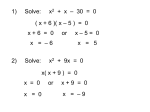Download Worksheet 31 (6

Worksheet 31 (6.1)
Chapter 6 Exponents and Radicals
6.1 Using Integers as Exponents
Summary 1:
If b is a nonzero real number, then: b0 = 1
If n is a positive integer and b is a nonzero real number, then: b-n =
1
b
Warm-up 1. Simplify:
a) 250 =
c) (x2y)0 =
b) (-92)0 =
d) -250 =
Problems - Simplify:
1. 80
3. -100
2. (-10)0
4. (ab2)0
Warm-up 2. Simplify:
1
a) a-3 =
( )
1
1
b) 3- 2 =
=
( ) ( )
120
n
c)
5
5
( )
=
= (5)
=
-3
1
y
 1 
( )
Problems - Simplify:
5. z -5
6.
2
b
7. 5-3
-4
Worksheet 31 (6.1)
Summary 2:
We can now restate the properties of exponents, presented in Chapter 3,
to include all integer exponents. We will also now name the properties.
If m and n are integers and a and b are real numbers, except b  0,
whenever it appears in a denominator, then:
1. bn  bm = bn + m
product of two powers
m
2. ( bn ) = bm n
power of a power
3. (ab )n = a n bn
power of a product
n
 a  an
4.   = n
b b
n
b
5. m = bn- m
b
power of a quotient
quotient of two powers
121
Warm-up 3. Simplify:
a) 3-5  33 = 3-5 + 3 = 3( ) =
b) ( 2-2 )-1 = 2(-1)(-2)= 2(
)
=
c) ( 5-2  2 )-1 = ( 5-2 )-1  (2 )-1 = 5(
(
 -4   -4 
d)  2-3  = 2 -1 = 2(
3-3  3
3 
-3
7
e) -5 = 7 -3-(-5)= 7 ( ) =
7
-1
-1
)
)
=
(
(
)
 2( ) =
(
(
)
)
)
)
Problems - Simplify:
8. 2  2
-6
 3-5 
9.  -4 
3 
-2
13
12. - 3
13
3
11. ( 5-1 )-2
-2
10. ( 7 -2  23 )-1
Worksheet 31 (6.1)
Warm-up 4. Perform the indicated operations and/or simplify. Express your
results using positive integral exponents only.
1
a) y -7  y3 = y( ) =
(
)
(
)
b) ( x-3 y 4 )-2 = ( x-3 )-2 ( y4 )-2 = x( ) y( ) =
(
)
-2
 y -5 
( y -5 )- 2 y(


= (
c)  -3  =
-2
y
( y -3 )
y 
)
)
= y(
- )
= y(
d) (2 x-3 y 2 ) (5 x-2 y -1 ) = 10 x-3 + (-2 ) y 2 + (-1)
= 10 x( ) y(
10( )
=
( )
-2
 14 a-3 b4 
-2
e) 
 = 7 a-3-1 b4-(-2) 
-2 
 2ab 
-2
=  7 a( ) b( ) 
= 7-2 a(
)
122
(
b
)
)
)
(
=
a
2 (
7 b
)
)
=
(
(
)
)
Problems - Perform the indicated operations and/or simplify. Express your
results using positive integral exponents only.
-5
13. a  a2
14. ( x-5 y6 )-3
 -3 
15.  z-4 
z 
-3
16. (-3 a-5 b ) ( 2 a4 b-3 )
-2
 18 -2 y3 
17.  x4 -1 
 6x y 
Worksheet 31 (6.1)
Warm-up 5. a) Simplify: 3-2 + 2-1 =
1
(
+
1
) ( )
1
1
=
+
( ) ( )
(
) (
)
+
=
18
18
(
)
=
18
b) Express as a single fraction involving positive exponents only:
1
1
-3
-2
x -y =
( ) ( )
( ) ( )
= 2 3- 2 3
x y x y
(
)
=
3
2
x y
Problems
18. Simplify: 5-1 + 2-2
19. Express as a single fraction involving positive exponents only: a-3 + b-2
123
Worksheet 32 (6.2)
6.2 Roots and Radicals
Summary 1:
To square a number means to use the number as a factor twice.
EX.
52 = 55 = 25 and (-7)2 = (-7)(-7) = 49
The square root of a number is one of its two equal factors.
EX. 5 is a square root of 25 because 55 = 25,
-5 is a square root of 25 because (-5)(-5) = 25.
The symbol  is called a radical sign and is used to designate the
nonnegative square root.
The radicand is the number under the radical sign.
EX.
in 25 the radicand is 25
The entire expression is called a radical.
25
- 25
- 25
indicates the nonnegative or principal square root of 25.
indicates the negative square root of 25.
is not a real number.
The following generalizations can be made:
1. Every positive real number has two square roots; one is positive and
2. Negative real numbers have no real number square roots because any
3. The square root of 0 is 0.
If a  0 and b  0, then b = a if and only if a2 = b;
a is called the principal square root of b.
Warm-up 1. Evaluate:
a) 81 =
c) - 64 =
124
the o
nonzero real
b)
0 =
d)
Problems- Evaluate:
1. 36
3. -
9
49
=
2. - 0
100
9
4.
121
Worksheet 32 (6.2)
To cube a number means to use the number as a factor three times.
EX.
33 = 333 = 27 and (-4)3 = (-4)(-4)(-4) = -64
A cube root of a number is one of its three equal factors.
EX. 3 is a cube root of 27 because 333 = 27
-4 is a cube root of -64 because (-4)(-4)(-4) = -64
3
designates the cube root of a number.
3
b = a if and only if a3 = b;
a is called the principal cube root of b or just the cube root of b.
The concept of root can be extended to fourth roots, fifth roots, and, in general, nth
roots.
The following generalizations can be made:
If n is an even positive integer, then the following statements are true:
1. Every positive real number has exactly two real nth roots, one
2. Negative real numbers do not have real nth roots.
If n is an odd positive integer greater than one, then the following statements
true:
1. Every real number has exactly one real nth root.
2. The real nth root of a positive number is positive.
3. The real nth root of a negative number is negative.
In general, n b = a if and only if an = b.
n
designates the principal nth root.
The n in the radical n b is called the index of the radical.
Summary 2:
Warm-up 2. Evaluate:
a)
3
- 27 =
125
positive and
are
b)
3
64
125
c)
4
16 =
=
Worksheet 32 (6.2)
Problems - Evaluate:
5. - 4 81
6.
3
7.
8
3
-
1
27
Summary 3:
Properties of Radicals
n
n
For any nonnegative number b, if n is any positive integer greater than one,
n
2
n
2
b = n b = b EX. 25 = 2 5 = 2 5 = 5
then:
For any negative number b, if n is an odd positive integer greater than one,
then:
 
n
 
3
3
b = b EX. - 8 = 3 (-2 ) = - 2
If n b and n c are real numbers, then:
1. n bc = n b n c
(The nth root of a product is equal to the product of the nth roots.)
b nb
2. n = n c  0
c
c
(The nth root of a quotient is equal to the quotient of the nth roots.)
Summary 4:
Simplest Radical Form
126
A radical is said to be in simplest radical form if the following conditions are
satisfied:
1. No fraction appears under a radical sign.
2. No radical appears in the denominator.
3. No radicand contains any perfect powers of the index.
Warm-up 3. Change to simplest radical form:
a) 4 124 =
40 = 4  10 =
b)
 10 =
10
Worksheet 32 (6.2)
c) 2 50 = 2 ( ) ( ) = 2( )
d) 21 18 = 21 ( ) ( ) = 21 ( )
e)
3
54 = 3 (
)(
)=
=
=
3
Problems - Change to simplest radical form:
8. 5 85
9. 75
10. 3 24
11. 23 28
12.
3
48
Summary 5:
The process of removing the radical from the denominator of a fraction is
127
called rationalizing the denominator. In this process the numerator and
denominator of the fraction are multiplied by a number which will make the
denominator become a rational number.
Warm-up 4. Simplify:
1
1 (
a)
=

2
2 (
(
7
7
3
=

=
12
12
3
(
b)
3
c)
( )
)
=
) ( )
3
5 35 34 3(
=

=
2 32 34 3(
)
)
)
)
=
3
=
( )
( )
( )
( )
Worksheet 32 (6.2)
d)
48
48
=
=
3
3
=
 Note: In part d, the problem was reducible to a perfect square, therefore did not have to be
rationalized.
Problems - Simplify:
13.
2
3
14.
5
32
3
15.
3
2
7
Summary 6:
Many real-world and geometric applications involve radical expressions.
One which will be demonstrated here is called Heron's Formula:
128
K = s (s - a) (s - b) (s - c)
This formula can be used to determine the area (K) of a triangle with sides
a,b,
c.
The letter s represents the semiperimeter of the triangle.
The
semiperimeter is found by taking the sum of the sides, and dividing by 2.
semiperimeter = s =
a+b+c
2
Warm-up 5. a) Find the area of a triangle with sides of length 8, 10 and 12.
(We must first find the semiperimeter):
a + b + c ( )+ ( )+ ( ) ( )
=
=
=
s=
2
2
2
K = s (s - a) (s - b) (s - c)
Worksheet 32 (6.2)
K = ( )    
K= (
K=
K=
)(
)(
)(
)
(Use a calculator and round to the nearest tenth.)
The area of the triangle is
square units.
Problems
16. Find the area of a triangular scarf with sides of 12 inches, 12 inches and 18
inches. (Round to the nearest tenth.)
129
Worksheet 33 (6.3)
6.3 Combining Radicals and Simplifying Radicals That Contain
Variables
Summary 1:
Only radicals with the same index and the same radicand can be added or
subtracted. (These are sometimes called like radicals.)
Radical expressions can be simplified by using the distributive property to
Warm-up 1. Simplify:
a) 4 3 - 27 - 75 = 4 3 - ( ) ( ) - ( ) ( )
=4 3 -( )
=
130
-( )
combine like
b)
1 3
3
5 - 51 3 40 = 31 3 5 - 51 - 3 ( ) ( )
= 31 3 5 - 51 ( )3
)3
= 31 3 5 - (
=
3
-
5
( ) ( ) 3
=
 5
15 
 15
3
=
5
Problems - Simplify:
1. 41 2 + 23 32
2. 5 3 3 + 2 3 24 - 3 81
Worksheet 33 (6.3)
 Note:
To avoid the necessity for absolute value when simplifying radicals containing variables,
we shall assume that all variables represent positive real numbers.
Summary 2:
To simplify radicals containing variables, the same basic approach is used
as with numerical factors. The variables are factored using the largest
possible perfect power of the index.
Warm-up 2. Simplify:
4
4
a) 75 x5 y = 25  3  x4  x1  y
b)
3
=
25 x4 y 4  (
=
(
48 x7 y 5 = 3 8 (
)
)
) x6 (
) y3 (
3
= 3 8 x6 y  3 (
=
3
(
Problems - Simplify:
3.
28 x7 y 3
131
)
)
)
4.
3
54 a4 b10
Summary 3:
To rationalize denominators containing variables under the radical,
multiply the numerator and denominator of the fraction by the same
radical to make the denominator become a perfect power of the index.
Worksheet 33 (6.3)
Warm-up 3. Simplify:
2a
a)
=
5b
2a
5b

5b
5b
(
)
=
=
2
b)
75 x
3
(
)
(
(
)
)
2
=
25  3  x2  x
2
=
( ) ( )
=
2
) (
(
(
=
(
3
3
3x
2
=
(
=
3x
2

3
(
)
3
(
)
33 (
)
(
)
3
)
)
)
(
3
3
)
) (
=
c)
)

132
(
)
(
)
=
Problems c
5.
3a
33 ( )
( )
Simplify:
Worksheet 33 (6.3)
5x
6.
8 y5
3
7.
3
7
2x
Warm-up 4. Simplify:
a) - 2 25 y + 36 y - 4
b) 3
45 x7 - 2 x
4 y =- 2( )
y +( )
=( )
y +( )
=
y
y -4( ) y
y -( )
y
9 ( ) x6 ( ) - 2 x 4 ( ) x4 ( )
20 x5 = 3
=3
9 x6 
= 3(
) (
(
)-2x
) - 2 x(
4 x4 
) (
(
)
)
=
(
)-
(
)
=
Problems - Simplify:
8. 2 64 a - 5 81 a
9. - 5
32 x3 + 4 x
50 x
Worksheet 34 (6.4)
6.4 Products and Quotients Involving Radicals
133
Summary 1:
The property n b c = n b n c can also be used to multiply radicals and
express the product in simplest form.
Warm-up 1. Multiply and simplify where possible:
=
a) 8  2 =

c)  5
b) 3

6  7
5 -2

2 =
3 =
=

d) 3 3
(
)(
)
= ( )( )
=
3
3
2 -4 4 =
=
( )
=


Problems - Multiply and simplify where possible:
1. 15  3
2. 5 10 - 3 2
3.

5

3  6
7


4.
Summary 2:
The distributive property can be used to find the product of radicals
involving binomials.
Worksheet 34 (6.4)
Warm-up 2. Multiply and simplify where possible.
a) 2 5 + 6 = 10 +


134
= 10 + (
= 10 +

b) 3
5 x 2 4 -5
)(
)

- 15 30 x2
6x =
=
(
=(
3
c)

)(

5- 6


e) 2 8 - 3 2
=
+(
=
+
)+
30
30
3
)(
)
8( )
3
3

7+ 3 = 5
 6
-


7+ 3 - 6
7+ 3
=
=
35 + 15 -
-
35 + 15 -
- ( )( )
=
35 + 15 -
-





2 +5 5 = 2 8 6 2 +5 5 - 3 2 6 2 +5 5
= 12 16 + 10 40 =
30
3
)(

) - 15 ( )
-
4 2 3 2 +3 3 6 = 2 3 8 +

)
=
=(
d)
)(
+ 10( )
-
-
-
= 12 ( ) +
=

( )(10) - ( ) ( ) -
+
Worksheet 34 (6.4)
f)

3- 2


3+ 2 = 3
=
=
=


3+ 2 - 2
+
-
-

3+ 2

-
 Note:
The problem in part f fit the special product pattern: (a + b)(a - b) = a2 - b2. Notice that
the final product contains no radical, therefore is rational. This concept is used in rationalizing
binomial denominators containing radicals.
Binomials such as 3 + 2 and 3 - 2 are called conjugates.




Problems - Multiply and simplify where possible.
3- 7
5. 6

6. 2


3a 5
4 a +4 5

135
7.
3

9 33 3 -23 2
8.

9.
5
2+ 5

7 -2 3

3 - 11
 5

7 +2 3

Summary 3:
To rationalize a denominator containing a binomial radical, multiply the
numerator and the denominator of the fraction by the conjugate of the
denominator.
Worksheet 34 (6.4)
Warm-up 3. Rationalize the denominator and simplify:
 3 +4 
-2
-2

=
 
a)
3 -4
3 - 4  3 + 4 
=
=
=
=
b)
x +1
=
x -2

-2



3 -( )
-( )
-2 3 -( )
( )-( )
-2
3 -(
( )
x +1 

x - 2 
=

- 2 3 +4
3 -4
3 +4


x +1
x -2
)
x +2
x +2


136




x +2
x +2


=
=
(
(
)+( )+(
( )-(
)+( )+(
( )-( )
)+(
)
)
)
Problems - Rationalize the denominator and simplify:
3
10.
5- 2
11.
2 x -5
x +3
Worksheet 35 (6.5)
6.5 Equations Involving Radicals
Summary 1:
Radical Equations
A radical equation is an equation containing radicals with variables in a
radicand.
To solve radical equations the following property is used:
Let a and b be real numbers and n be a positive integer,
If a = b, then an = bn
(This property states that both sides of an equation can be raised to a
positive integral power.)
This process will sometimes produce answers that do not satisfy the original
equation. These extra solutions are called extraneous solutions.
137
Summary 2:
To Solve Radical Equations Containing One Radical
1. Isolate the radical on one side of the equation.
2. Raise both sides of the equation to the power corresponding to the index
the radical.
3. Solve the resulting linear or quadratic equation.
4. Check all solutions in the original equation for extraneous solutions.
Warm-up 1. Solve:
3 x +1 -7 = 0
a)

Check:
of
3 ( )+ 1 - 7 ¿0
- 7 ¿0
3 x +1 =

2
2
3 x+1 =(
=
x=
-
)
¿0
Solution Set = {
= 0
}
x=
Worksheet 35 (6.5)
3
b)

(
)(
3
2
x -9 =-2
2
x -9
=
)
138

( )
= - 2 (
=0
=0
)
= 0 or
=0
x =
or x =
Check:
3
( )2 - 9 ¿ - 2
or
3
( )2 - 9 ¿ - 2
( ) - 9 ¿- 2
3
3
3
3
¿- 2
= -2

¿- 2
= -2
Solution Set = {
c)
( ) - 9 ¿- 2
}
a+3 = a - 3
a+3

( )
= ( a - 3 )(
)
=
+
0
=
+
0
= (a )(a )
a= 0 or a =0
a=
or a
=
Check:
( ) + 3 ¿ ( ) - 3 or ( ) + 3 ¿ ( ) - 3
¿
=
Solution Set = {
¿

}
Problems - Solve:
1. 2b - 3 - 5 = 0
Worksheet 35 (6.5)
2. 4 2 x - 6 = 2
3.
2 y+5 = y - 5
Summary 3:
To Solve Radical Equations Containing Two Radicals
139
1. Separate the two radicals, one on each side of the equation.
2. Raise each side of the equation to the power corresponding to the index
the radical.
3. If a radical still remains in the problem, isolate the radical.
4. Raise each side of the equation to the power corresponding to the index
the radical.
5. Solve the resulting linear or quadratic equation.
6. Check all solutions in the original equation for extraneous solutions.
Warm-up 2. Solve:
a) x + 4 - x - 4 = 2
x+4 =

x+4

( )
)2
of
+2
=
=
=
=
(
of
=
+2
(
)
x-4 +
+
x-4

x-4
x-4

(
)
=
=x
Worksheet 35 (6.5)
Check:
( )+ 4 -
(
)- 4 ¿2
-
-
¿2
¿ 2
=2
Solution Set= {
Problem - Solve:
140
}
4.
x + 12 + x + 4 = 4
Worksheet 36 (6.6)
6.6 Merging of Exponents and Roots
Summary 1:
Rational Exponents
141
If b is a real number, n is a positive integer greater than one and n b
1
exists then: b n = n b
m
If is a rational number, where n is a positive integer greater than one
and
n
b
is
a
real
number
such
that n b exists,
then:
m
m


m
bn = n b = n b
Notice that the denominator of the exponent, n, becomes the index of the
radical; and the numerator of the exponent, m, becomes the exponent of
Warm-up 1. Simplify:
1
a) 812 = (
)=
b) - 64  = 3 (
1
3
)=
1
4
(
 16 
c)   = 4
(
 81 
3
d) 9 2 =

1
e) (16 )- 4 =

)
=
)
3
3
)=
) =(
(
1
1
4
=
(16 )
1
2
f) 125- 3 =
2 =
( )3

1
4
(
)
1
3
(
)
=

1
(
( )
)
=
1
1
=
( )
( )
( )
Worksheet 36 (6.6)
142
the radicand
Problems - Simplify:
1
1. 49 2
1
2. (-27 )3
1
 1 4
3.  
 16 
3
4. 16 2
1
5. (36 )- 2
4
6. (-8 )- 3
Summary 2:
Problems can be written in exponential form or radical form. Sometimes it is
helpful to be able to switch from one form to the other.
Warm-up 2. Write in radical form:
2
a) y 3 = (
)
y
3
b) 2 x 4 = 2 (
1
( )
)
y
3
c) a 2 b 2 = (
4
5
( )
)
d) ( a + b ) = (
)
(a + b )(
)
Problems - Write in radical form:
1
5
2
7. a 6
8. x 3 y 3
2
10. (x - y )7
Worksheet 36 (6.6)
Warm-up 3. Write using positive rational exponents:
a)
3
( )
( )
( )
)
a b = ( a b )( ) = a( ) b(
143
2
9. 5 x 5
5
b)


( )
( )
)
2 3
3
x y = x2 y ( ) = x (
( )
)
y(
c) 2 4  a - b 3 = 2  a - b (
( )
)
Problems - Write using positive rational exponents:
11. 5 x4 y
12.
4
13. 3
2x
( x + y )3
Summary 3:
The basic properties of exponents are used to simplify expressions containing
rational exponents.
Warm-up 4. Simplify, expressing results using positive exponents only:
3
3
1
1
a) 5 x 2 2 x 4 = ( 5  2 ) x 2  x 4
1+3
=
x2 4




=
=
 a3 
 1 
 a4 
2-1
a3 4
=
a 12
18 a 3  18 
b)

1 =
6 a4  6 
2
4 x
c)  2
5
 y
1
2
2


 = 4x
2

y5

1
2

 
=
2
(
x
( ) ( )
+
4
4
( )
=
=
x
( )
4
2
( ) ( )
12
2

4
x 
1
2
=
( )
a 12
Worksheet 36 (6.6)
( )
( )
)
y(
) x(
)
( )
y( )
Problems - Simplify, expressing results using positive exponents only:
1
1
14. 3 y 3 5 y 4



3
12 x 5
15.
2
6 x3
144
 15 x 4 

16. 
1
 3 x3 
3
3
Summary 4:
Some radicals can be multiplied and divided, even if they have a different
index, by changing to exponential form, using the properties of
exponents, and changing back to radical form.
Warm-up 5. Perform the indicated operations and express the answer in simplest
radical form.
1
1
a) 3  4 3 = 3 2  3 4
( ) ( )
+
) ( )
= 3(
( )
)
= ( ) 3( ) = ( ) (
= 3(
)
Worksheet 36 (6.6)
3
b)
1
1
3
2 23
= 1= 2 1
8 8 2  23 2
1
3
= 2( )
2( )
1 (
)
)
= 23 - (
=2
( ) ( )
6
6
( )
)
= 2(
=(
=
1
)
( )
2
1
6
2
Problems - Perform the indicated operations and express the answer in simplest
radical form:
145
17.
18.
2 2
5
3
25
5
Worksheet 37 (6.7)
6.7 Scientific Notation
Summary 1:
Scientific Notation
Scientific notation or scientific form is used to more conveniently
represent very small or very large numbers.
To express a number in scientific notation, write the number as a product
ofa
number between 1 and 10 and an integral power of 10. (N) (10)k
EX. (2.5) (10)3
(3.62) (10)-4
Procedure to change from ordinary notation to scientific notation:
Summary 2:
146
1. Write the number as the product of a number between 1 and 10 and a
power of ten. (There should be only one digit to the left of the decimal.)
2. The exponent of the 10 corresponds to the number of places the decimal
point moves when changing the number to a number between 1 and 10.
3. The exponent is:
- negative if the original number is less than 1: 0.0036 = (3.6) (10)-3
(Decimal moved to the right.)
- positive if the original number is greater than 1: 563 = (5.63) (10)2
(Decimal moved to the left.)
- 0 if the original number is between 1 and 10: 9.38 = (9.38) (10)0
(Decimal did not move.)
Warm-up 1. Write in scientific notation:
a) 476 = (4.76) (10)(
)
b) 0.000096456 = (9.645) (10)(
c) 29,000,000 = (
d) 0.0136579 = (
) (10)(
) (10)(
Worksheet 37 (6.7)
Problems - Write in scientific notation:
147
)
)
)
1. 5,611
2. 0.000319
3. 520,000,000,000
4. 0.000000872
5. 3.51267
Summary 3:
Procedure to change from scientific notation to ordinary notation:
1. Move the decimal point the number of places indicated by the exponent
2. The decimal point moves to the right if the exponent is positive:
(3.19) (10)3 = 3,190
3. The decimal point moves to the left if the exponent is negative:
EX. (2.793) (10)-2 = 0.02793
of the 10.
EX.
Warm-up 2. Write in ordinary notation:
a) (9.345) (10)5 =
(Decimal moves 5 places to the right.)
b) (2.15) (10)-4 =
(Decimal moves 4 places to the left.)
c) (6) (10)3 =
d) (2) (10)-4 =
Problems - Write in ordinary notation:
148
6. (2.49678) (10)6
7. (9) (10)-2
8. (3.1864) (10)-3
9. (7) (10)4
Worksheet 37 (6.7)
Summary 4:
To simplify numerical calculations, change the numbers to scientific notation
and use the properties of exponents.
Warm-up 3. Perform the indicated operations using scientific notation and the
properties of exponents:
a) (25,600) (1,900)
= (2.56) (10)4 (1.9) (10)3
= (2.56) (1.9) (10)4 (10)3
=(
) (10)( )
=
) (10)( ) (
) (10)(
( )
)(
) (10) (10)(
b) (0.000341) (0.0019) = (
=(
) (10)(
=(
=
c)
96,000,000 ( 9.6 ) ( 10 )(
=
0.032
( 3.2 ) ( 10 )(
= ( ) (10)(
)
)
)
)
)
)
=
d)
( 70,000 ) ( 0.0005 )
( 7 ) ( 10 )4 ( 5 ) ( 10 ) -4
=
( 0.0025 ) ( 56,000 ) ( ) ( 10 )-3 ( 5.6 ) ( 10 )(
149
)
=
( 7 ) ( 5 ) ( 10 )4 ( 10 )-4
(
) ( 5.6 ) ( 10 )-3 ( 10 )(
=
(
(
) ( 10 )(
) ( 10 )(
)
)
)
=
Worksheet 37 (6.7)
Problems - Perform the indicated operations using scientific notation and
properties of exponents:
10. (8,942) (1,500,000)
11. (0.00025) (0.006)
12.
1,500,000
0.00003
13.
( 90,000 ) ( 0.0015 )
( 125,000 ) ( 0.0027 )
Summary 5:
Scientific Notation and Calculators
150
Most calculators will automatically display answers in scientific notation if the
answer exceeds the calculator's display capabilities.
420,0002 will be displayed as 1.764 E11 on a graphing calculator
420,0002 will be displayed as 1.764 11 on most scientific calculators.
Many calculators also have a key to select scientific notation mode. When
is selected, all answers will be displayed in scientific notation.
this
Many calculators also allow you to enter a number in scientific notation by
an enter-the-exponent key. (EE or E EX or EXP)
using
It is important that you have a thorough understanding of the capabilities of
calculator.
your
151