Theoretical prediction of the nondiffractive propagation of sonic
... given by the set R = 兵R = n1a1 + n2a2 ; n1 , n2 苸 N其 of twodimensional lattice vectors R, which are generated by the primitive translations a1 and a2. The corresponding reciprocal lattice is defined though G = 兵G : G · R = 2n ; n 苸 N其. A possible way of solving Eq. 共3兲 is by means of the plane-wave ...
... given by the set R = 兵R = n1a1 + n2a2 ; n1 , n2 苸 N其 of twodimensional lattice vectors R, which are generated by the primitive translations a1 and a2. The corresponding reciprocal lattice is defined though G = 兵G : G · R = 2n ; n 苸 N其. A possible way of solving Eq. 共3兲 is by means of the plane-wave ...
Research Article Generalized Buneman Dispersion
... new types of instabilities. The original “8”-like imaginary branch broke into two parts and new “8”-like imaginary curve appears in the vertical direction of the (ω, k) plane. Furthermore the dispersion relation gives 4 new imaginary branches, which are only very weakly dependent on the perturbation ...
... new types of instabilities. The original “8”-like imaginary branch broke into two parts and new “8”-like imaginary curve appears in the vertical direction of the (ω, k) plane. Furthermore the dispersion relation gives 4 new imaginary branches, which are only very weakly dependent on the perturbation ...
1. Twelve equal charges q are situated in the corners of a regular 12
... a horizontal Circular orbit with tangential velocities v and 2v respectively. Between collisions the spheres move with constant speeds. The number of elastic collisions the spheres will make before they reach the point A again is A) 2 ...
... a horizontal Circular orbit with tangential velocities v and 2v respectively. Between collisions the spheres move with constant speeds. The number of elastic collisions the spheres will make before they reach the point A again is A) 2 ...
Entropy change due to mixing , T . Evaluate
... a) Pretending that there is no conservation law for the number of nucleons, calculate the partition function at temperature T. (Nucleons are fermions). b) Calculate the average energy density and average particle density. c) In view of (a) and (b), discuss the necessety for a consevation law for the ...
... a) Pretending that there is no conservation law for the number of nucleons, calculate the partition function at temperature T. (Nucleons are fermions). b) Calculate the average energy density and average particle density. c) In view of (a) and (b), discuss the necessety for a consevation law for the ...
Part II
... Device transconductance kp=µnCoxW/L is larger for NMOS than PMOS In CMOS for compensation of the mobility differences use Wp>Wn ...
... Device transconductance kp=µnCoxW/L is larger for NMOS than PMOS In CMOS for compensation of the mobility differences use Wp>Wn ...
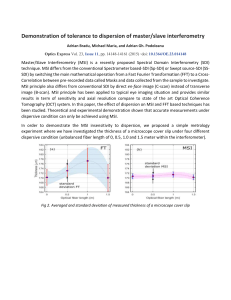
Demonstration of tolerance to dispersion of master/slave interferometry
... image (B-scan). MSI principle has been applied to typical eye imaging situation and provides similar results in term of sensitivity and axial resolution compare to state of the art Optical Coherence Tomography (OCT) system. In this paper, the effect of dispersion on MSI and FFT based techniques has ...
... image (B-scan). MSI principle has been applied to typical eye imaging situation and provides similar results in term of sensitivity and axial resolution compare to state of the art Optical Coherence Tomography (OCT) system. In this paper, the effect of dispersion on MSI and FFT based techniques has ...
Gauss` Law and Applications
... ri rj • Fij is force on i due to presence of j and acts along line of centres rij. If qi qj are same sign then repulsive force is in ri direction shown • Inverse square law of force ...
... ri rj • Fij is force on i due to presence of j and acts along line of centres rij. If qi qj are same sign then repulsive force is in ri direction shown • Inverse square law of force ...
Density of states
In solid-state and condensed matter physics, the density of states (DOS) of a system describes the number of states per interval of energy at each energy level that are available to be occupied. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not discrete like a spectral density but continuous. A high DOS at a specific energy level means that there are many states available for occupation. A DOS of zero means that no states can be occupied at that energy level. In general a DOS is an average over the space and time domains occupied by the system. Localvariations, most often due to distortions of the original system, are often called local density of states (LDOS). If the DOS of an undisturbedsystem is zero, the LDOS can locally be non-zero due to the presence of a local potential.