Decision One:
... Notes: Begin with an 11” X 17” piece of paper folded in thirds lengthwise, then a two inch tab and fold into fourths in the other direction. Each column is to be labeled with the four operations and proper notes will be filled in the appropriate columns. ...
... Notes: Begin with an 11” X 17” piece of paper folded in thirds lengthwise, then a two inch tab and fold into fourths in the other direction. Each column is to be labeled with the four operations and proper notes will be filled in the appropriate columns. ...
Quadratic equations File
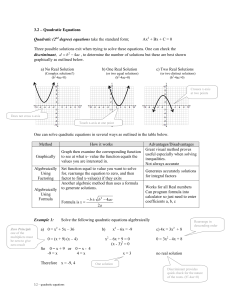
... The most significant part of the formula is the expression b 2 4ac Note: If b2 > 4ac the roots can be found and will not be equal. If b2 = 4ac the roots can be found and will be equal. If b2 < 4ac the roots to negative numbers are involved:these are referred to as imaginary roots and will be inves ...
... The most significant part of the formula is the expression b 2 4ac Note: If b2 > 4ac the roots can be found and will not be equal. If b2 = 4ac the roots can be found and will be equal. If b2 < 4ac the roots to negative numbers are involved:these are referred to as imaginary roots and will be inves ...
7.EE.1final
... Hand out index cards to all students with various “terms” on them. Have students find their “match” which would be a student with a “like term.” Students should combine their like terms. Identify the GCF of two given composite numbers. Write an addition expression using the two given numbers. Demons ...
... Hand out index cards to all students with various “terms” on them. Have students find their “match” which would be a student with a “like term.” Students should combine their like terms. Identify the GCF of two given composite numbers. Write an addition expression using the two given numbers. Demons ...
Reference Sheet
... Square Number: A number that has a factor that is multiplied by itself. For example: 9 is a square number. 9 is the product of 3 x 3 Some other square numbers include: 4=2x2 16 = 4 x4 25 = 5 x 5 36 = 6 x 6 If you draw an array of any of the above square numbers, can you see that the length of the ro ...
... Square Number: A number that has a factor that is multiplied by itself. For example: 9 is a square number. 9 is the product of 3 x 3 Some other square numbers include: 4=2x2 16 = 4 x4 25 = 5 x 5 36 = 6 x 6 If you draw an array of any of the above square numbers, can you see that the length of the ro ...
FERM - Interjetics
... many elementary college algebra books. As all mathematicians know the binomial coefficients Bj have the important interpretation of being the number of finite elements of size j from a set of size n. Therefore, binomial coefficients are always integral and nonzero. STATEMENT OF FERMAT'S LAST THEOREM ...
... many elementary college algebra books. As all mathematicians know the binomial coefficients Bj have the important interpretation of being the number of finite elements of size j from a set of size n. Therefore, binomial coefficients are always integral and nonzero. STATEMENT OF FERMAT'S LAST THEOREM ...
FINITE FIELDS OF THE FORM GF(p)
... The AES algorithm uses arithmetic in the finite field GF(28), p=2, n=8, with the irreducible polynomial m(x)= x 8 x 4 x 3 x 1. It can be shown that the set of all polynomials modulo an irreducible nth degree polynomial m(x) satisfies the axioms in Fig. 4.1 and thus forms a finite field. Furt ...
... The AES algorithm uses arithmetic in the finite field GF(28), p=2, n=8, with the irreducible polynomial m(x)= x 8 x 4 x 3 x 1. It can be shown that the set of all polynomials modulo an irreducible nth degree polynomial m(x) satisfies the axioms in Fig. 4.1 and thus forms a finite field. Furt ...
FINITE FIELDS OF THE FORM GF(p)
... The AES algorithm uses arithmetic in the finite field GF(28), p=2, n=8, with the irreducible polynomial m(x)= x 8 x 4 x 3 x 1. It can be shown that the set of all polynomials modulo an irreducible nth degree polynomial m(x) satisfies the axioms in Fig. 4.1 and thus forms a finite field. Furt ...
... The AES algorithm uses arithmetic in the finite field GF(28), p=2, n=8, with the irreducible polynomial m(x)= x 8 x 4 x 3 x 1. It can be shown that the set of all polynomials modulo an irreducible nth degree polynomial m(x) satisfies the axioms in Fig. 4.1 and thus forms a finite field. Furt ...
Section 5.6 Solving Quadratic Equations by Factoring
... Solving a Quadratic Equation by Factoring ...
... Solving a Quadratic Equation by Factoring ...
In this chapter, you will be able to
... Identify the Zeros of a Polynomial and Their Multiplicity Analyze the Graph of a Polynomial Find the Domain of a Rational Function Determine the Vertical Asymptotes of a Rational Function Analyze the Graph of a Rational Function Utilize the Remainder and Factor Theorems Use Decartes’ Rule of Signs t ...
... Identify the Zeros of a Polynomial and Their Multiplicity Analyze the Graph of a Polynomial Find the Domain of a Rational Function Determine the Vertical Asymptotes of a Rational Function Analyze the Graph of a Rational Function Utilize the Remainder and Factor Theorems Use Decartes’ Rule of Signs t ...
Factorization
In mathematics, factorization (also factorisation in some forms of British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.The aim of factoring is usually to reduce something to “basic building blocks”, such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra. Viète's formulas relate the coefficients of a polynomial to its roots.The opposite of polynomial factorization is expansion, the multiplying together of polynomial factors to an “expanded” polynomial, written as just a sum of terms.Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function. This situation is generalized by factorization systems.