x - Barnstable Academy
... polynomial has n linear factors. This is formally stated as the Linear Factorization Theorem. ...
... polynomial has n linear factors. This is formally stated as the Linear Factorization Theorem. ...
Polynomials
... The degree of a polynomial is the highest x power in the expression. Add or subtract polynomials by column addition or subtraction, or by collecting like terms. Multiply polynomials using any method that helps you to remember to multiply every term in one expression by every term in the other. Solve ...
... The degree of a polynomial is the highest x power in the expression. Add or subtract polynomials by column addition or subtraction, or by collecting like terms. Multiply polynomials using any method that helps you to remember to multiply every term in one expression by every term in the other. Solve ...
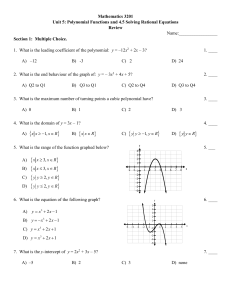
Mathematics 3201 Unit 5: Polynomial Functions and 4.5 Solving
... Sketch a possible graph of polynomial functions that satisfy each set of characteristics: A) Quadratic, one x-intercept, negative ...
... Sketch a possible graph of polynomial functions that satisfy each set of characteristics: A) Quadratic, one x-intercept, negative ...
The Coinvariant Algebra in Positive Characteristic
... We define a new action of a regular element c ∈ G on S := k̄ ⊗k S. Let cv = ζv where ζ ∈ k̄ × and v is regular. The order of c is divisible by the order of ζ (and in fact these orders are equal when S G is polynomial). Let c act on S n as multiplication by ζ n . Thus c acts on S ⊗S G k̄. The action ...
... We define a new action of a regular element c ∈ G on S := k̄ ⊗k S. Let cv = ζv where ζ ∈ k̄ × and v is regular. The order of c is divisible by the order of ζ (and in fact these orders are equal when S G is polynomial). Let c act on S n as multiplication by ζ n . Thus c acts on S ⊗S G k̄. The action ...
..
... 4. Let V .be the vector space of n x n matrices over IR. Consider the linear operator S:V -t V given by S(A) = (1/2)(A + AT), where T denotes . - transpose. Compute the rank and nullity of S. 5. Give n x n matrices over e that ha~e the following properties: i. the characteristic polynomial is (x + 1 ...
... 4. Let V .be the vector space of n x n matrices over IR. Consider the linear operator S:V -t V given by S(A) = (1/2)(A + AT), where T denotes . - transpose. Compute the rank and nullity of S. 5. Give n x n matrices over e that ha~e the following properties: i. the characteristic polynomial is (x + 1 ...
Box Method
... The student finds specific function values, simplifies polynomial expressions, transforms and solves equations, and factors as necessary in problem situations. (B) The student uses the commutative, associative, and distributive properties to simplify algebraic expressions. B. ...
... The student finds specific function values, simplifies polynomial expressions, transforms and solves equations, and factors as necessary in problem situations. (B) The student uses the commutative, associative, and distributive properties to simplify algebraic expressions. B. ...
Note One
... 1. Bezout’s lemma: If a, b are two positive integers, then there exist x, y ∈ Z such that ax + by = gcd(a, b). 2. Bezout’s lemma for polynomials: If f (x), g(x) are two univariate polynomials in F[x], where F is one of R[x], Q[x], Zp [x], then there exist polynomials u(x), v(x) in F[x] such that f ( ...
... 1. Bezout’s lemma: If a, b are two positive integers, then there exist x, y ∈ Z such that ax + by = gcd(a, b). 2. Bezout’s lemma for polynomials: If f (x), g(x) are two univariate polynomials in F[x], where F is one of R[x], Q[x], Zp [x], then there exist polynomials u(x), v(x) in F[x] such that f ( ...
FINAL EXAM
... (a) Find the remainder when f (x) = x6 − 3x4 + 5 is divided by g(x) = x − 2 in Q[x]. ...
... (a) Find the remainder when f (x) = x6 − 3x4 + 5 is divided by g(x) = x − 2 in Q[x]. ...
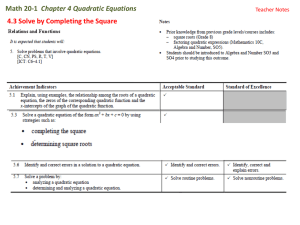
Solving Poly. Eq.
... Though many proofs are known to mathematicians, there are none known that do not involve calculus or another branch or higher mathematics. Now you have something to look forward to! Poly 12.9 ...
... Though many proofs are known to mathematicians, there are none known that do not involve calculus or another branch or higher mathematics. Now you have something to look forward to! Poly 12.9 ...
Slide 1
... The Rational Zero Theorem gives a list of possible rational zeros of a polynomial function. Equivalently, the theorem gives all possible rational roots of a polynomial equation. Not every number in the list will be a zero of the function, but every rational zero of the polynomial function will appea ...
... The Rational Zero Theorem gives a list of possible rational zeros of a polynomial function. Equivalently, the theorem gives all possible rational roots of a polynomial equation. Not every number in the list will be a zero of the function, but every rational zero of the polynomial function will appea ...
TRANSCENDENCE BASES AND N
... Reversing the roles of {xi} and {yj} in the lemma, you see that any two finite transcendence bases have the same cardinality. The lemma also implies that if one transcendence base is finite then so is any other. PROOF OF LEMMA: By the hypothesis on {yj}, x1 satisfies some non-trivial polynomial P(yj ...
... Reversing the roles of {xi} and {yj} in the lemma, you see that any two finite transcendence bases have the same cardinality. The lemma also implies that if one transcendence base is finite then so is any other. PROOF OF LEMMA: By the hypothesis on {yj}, x1 satisfies some non-trivial polynomial P(yj ...
Section 3.6 A Summary of Curve Sketching Slant (Oblique) Asymptote
... Section 3.6 A Summary of Curve Sketching ...
... Section 3.6 A Summary of Curve Sketching ...
Algebra1 - Tramore maths circle
... We have no formula for this and doing it using brackets would be v. tricky! If we can find one root of the equation (one value of x that works) then we can reduce the problem to solving a quadratic equation – then we can use the formula. Like finding the factors of 154. This is made easier if we kno ...
... We have no formula for this and doing it using brackets would be v. tricky! If we can find one root of the equation (one value of x that works) then we can reduce the problem to solving a quadratic equation – then we can use the formula. Like finding the factors of 154. This is made easier if we kno ...
WORD version
... 3. A positive integer is written on each face of a cube. To each vertex, we assign the product of the numbers written on the three faces meeting at that vertex. The sum of the numbers assigned to the vertices is 1001. What is the sum of the numbers written on the faces ? ...
... 3. A positive integer is written on each face of a cube. To each vertex, we assign the product of the numbers written on the three faces meeting at that vertex. The sum of the numbers assigned to the vertices is 1001. What is the sum of the numbers written on the faces ? ...
Factorization
In mathematics, factorization (also factorisation in some forms of British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.The aim of factoring is usually to reduce something to “basic building blocks”, such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra. Viète's formulas relate the coefficients of a polynomial to its roots.The opposite of polynomial factorization is expansion, the multiplying together of polynomial factors to an “expanded” polynomial, written as just a sum of terms.Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function. This situation is generalized by factorization systems.