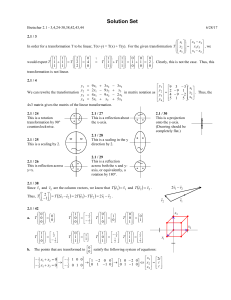
A I AI =
... Property 4: if A and B are similar, then det( A) det( B) Prove. Since A and B are similar, there is a nonsingular matrix S , such that A S 1BS det( A) det( S 1BS ) det( S 1 ) det( B) det( S ) det( B) since det(S 1 ) ...
... Property 4: if A and B are similar, then det( A) det( B) Prove. Since A and B are similar, there is a nonsingular matrix S , such that A S 1BS det( A) det( S 1BS ) det( S 1 ) det( B) det( S ) det( B) since det(S 1 ) ...
ex.matrix - clic
... Each row of the matrix is a vector ‘representing’ that customer. We can use these vectors to compare customers with each other. One way to do this is to multiply the matrix by its transpose. The transpose of the matrix is another matrix in which the rows have become the columns and viceversa: > t(ex ...
... Each row of the matrix is a vector ‘representing’ that customer. We can use these vectors to compare customers with each other. One way to do this is to multiply the matrix by its transpose. The transpose of the matrix is another matrix in which the rows have become the columns and viceversa: > t(ex ...
Condition estimation and scaling
... If we did want to form A−1 explicitly, the usual approach is to compute P A = LU , then use that factorization to solve the systems Axk = ek , where ek is the kth column of the identity matrix and xk is thus the kth column of the identity matrix. As discussed last time, forming the LU factorization ...
... If we did want to form A−1 explicitly, the usual approach is to compute P A = LU , then use that factorization to solve the systems Axk = ek , where ek is the kth column of the identity matrix and xk is thus the kth column of the identity matrix. As discussed last time, forming the LU factorization ...
Multivariable Linear Systems and Row Operations
... A multivariable linear system is a system of linear equation in two or more variables. The substitution and elimination methods you have previously learned can be used to convert a multivariable linear system into an equivalent system in triangular or row-echelon form. ...
... A multivariable linear system is a system of linear equation in two or more variables. The substitution and elimination methods you have previously learned can be used to convert a multivariable linear system into an equivalent system in triangular or row-echelon form. ...
Sheet 9
... Broadcasting happens in the vector quantization (VQ) algorithm used in information theory, classification, and other related areas. The basic operation in VQ finds the closest point in a set of points, called codes in VQ jargon, to a given point, called the observation. In a very simple two-dimensio ...
... Broadcasting happens in the vector quantization (VQ) algorithm used in information theory, classification, and other related areas. The basic operation in VQ finds the closest point in a set of points, called codes in VQ jargon, to a given point, called the observation. In a very simple two-dimensio ...
A.1 Summary of Matrices
... where the jth col consists of components of eigenvector e j. For the transformation to be unitary, the eigenvectors must be orthonormal (orthogonal and normalized). A.3 ...
... where the jth col consists of components of eigenvector e j. For the transformation to be unitary, the eigenvectors must be orthonormal (orthogonal and normalized). A.3 ...
finm314F06.pdf
... (d) Show from de nition that if λ is an eigenvalue of invertible A, then 1/λ is an eigenvalue of A−1 . ...
... (d) Show from de nition that if λ is an eigenvalue of invertible A, then 1/λ is an eigenvalue of A−1 . ...
Honors Linear Algebra (Spring 2011) — Homework 5
... • Problems marked with [M] involve the use of MATLAB. You must submit the commands you use as well as all output from MATLAB as part of the answer to such a problem. You are welcome to email me these commands and output files. If you do email me, name the file(s) using your first and last names. For ...
... • Problems marked with [M] involve the use of MATLAB. You must submit the commands you use as well as all output from MATLAB as part of the answer to such a problem. You are welcome to email me these commands and output files. If you do email me, name the file(s) using your first and last names. For ...
1. (14 points) Consider the system of differential equations dx1 dt
... 7. (15 points) Determine whether the following statements are true or false. As usual, briefly justify your answer. Your answer will be graded on its clarity and completeness. (a) If ~v1 , ~v2 and ~v3 are linearly independent vectors in R3 then so are w ~ 1 = ~v1 + ~v2 + 2~v3 , ...
... 7. (15 points) Determine whether the following statements are true or false. As usual, briefly justify your answer. Your answer will be graded on its clarity and completeness. (a) If ~v1 , ~v2 and ~v3 are linearly independent vectors in R3 then so are w ~ 1 = ~v1 + ~v2 + 2~v3 , ...
Additional File 3 — A sketch of a proof for the
... For every pair of states i and j, there is a walk i, 1, 1, · · · , 1, 2, 3, · · · , j − 1, j from i to j of length N with non-zero probability. Thus, the transition matrix T is primitive. By the Perron-Frobenius theorem [1], there exists an equilibrium state vector ⃗v = (v1 , v2 , · · · , vN ), such ...
... For every pair of states i and j, there is a walk i, 1, 1, · · · , 1, 2, 3, · · · , j − 1, j from i to j of length N with non-zero probability. Thus, the transition matrix T is primitive. By the Perron-Frobenius theorem [1], there exists an equilibrium state vector ⃗v = (v1 , v2 , · · · , vN ), such ...
Non-negative matrix factorization

NMF redirects here. For the bridge convention, see new minor forcing.Non-negative matrix factorization (NMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix V is factorized into (usually) two matrices W and H, with the property that all three matrices have no negative elements. This non-negativity makes the resulting matrices easier to inspect. Also, in applications such as processing of audio spectrograms non-negativity is inherent to the data being considered. Since the problem is not exactly solvable in general, it is commonly approximated numerically.NMF finds applications in such fields as computer vision, document clustering, chemometrics, audio signal processing and recommender systems.