07 some irreducible polynomials
... [1.0.3] Example: x2 + 1 is irreducible over k = Z/p for any prime p = 3 mod 4. Indeed, if x2 + 1 had a linear factor then the equation x2 + 1 = 0 would have a root α in k. This alleged root would have the property that α2 = −1. Thus, α 6= 1, α 6= −1, but α4 = 1. That is, the order of α in k × is 4. ...
... [1.0.3] Example: x2 + 1 is irreducible over k = Z/p for any prime p = 3 mod 4. Indeed, if x2 + 1 had a linear factor then the equation x2 + 1 = 0 would have a root α in k. This alleged root would have the property that α2 = −1. Thus, α 6= 1, α 6= −1, but α4 = 1. That is, the order of α in k × is 4. ...
Chapter 9 Quadratic Equations and Functions
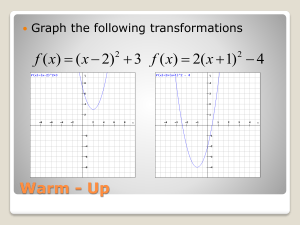
... moves to the left - if h is added to x moves to the right - if h is subtracted from x Vertical Translation - k moves up - if k is positive moves down - if k is negative a - reflection and dilation a is positive and opens up or negative and opens down a > 1 stretched vertically or 0 < a < 1 is compre ...
... moves to the left - if h is added to x moves to the right - if h is subtracted from x Vertical Translation - k moves up - if k is positive moves down - if k is negative a - reflection and dilation a is positive and opens up or negative and opens down a > 1 stretched vertically or 0 < a < 1 is compre ...