38A - Canal Winchester Schools
... 15. Three times some number decreased by 8 is -14. 16. The product of six and a number minus thirteen is equal to nineteen. 17. Six less than one fourth times a number equals two. 18. Five times the sum of some number and three is the same as thirty-five. ...
... 15. Three times some number decreased by 8 is -14. 16. The product of six and a number minus thirteen is equal to nineteen. 17. Six less than one fourth times a number equals two. 18. Five times the sum of some number and three is the same as thirty-five. ...
College Algebra Lecture Notes, Section 1.6
... C. Radical Equations and Equations with Rational Exponents Solving a radical equation with one radical expression: Isolate the radical expression (i.e., get it on one side of the equation by itself with all other terms on the other side). Raise both sides of the equation to the power of the inde ...
... C. Radical Equations and Equations with Rational Exponents Solving a radical equation with one radical expression: Isolate the radical expression (i.e., get it on one side of the equation by itself with all other terms on the other side). Raise both sides of the equation to the power of the inde ...
$doc.title
... The goal of middle school mathematics is to extend the strong foundational knowledge developed in elementary school to new topics as students prepare for high school. Students build on their previous un ...
... The goal of middle school mathematics is to extend the strong foundational knowledge developed in elementary school to new topics as students prepare for high school. Students build on their previous un ...
Diagnostic TEST #1
... Determine the rate of change and initial value of the function from a description of a relationship or from two (x,y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of ...
... Determine the rate of change and initial value of the function from a description of a relationship or from two (x,y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of ...
... 1. Solve equations containing rational expressions. We spent quite a little time in Chapter 2 working with equations that contained fractions. Solving a rational equation with a variable in the denominator is solved the same way with the addition of one step. We must keep in mind that the denominato ...
Hon Alg 2: Unit 6 SYSTEMS OF EQUATIONS A system of equations
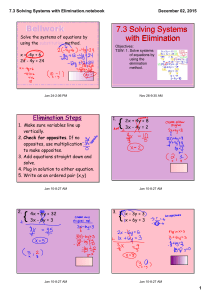
... Method #3: ELIMINATION - eliminate one variable from both equations STEP #1: Put both equations in SAME FORM (Ax + By = C) STEP #2: SELECT A VARIABLE to eliminate (x or y) STEP #3: As needed, make that variable in both equations have same coefficients and opposite signs (ex: -3x and 3x) by MULTIPLIC ...
... Method #3: ELIMINATION - eliminate one variable from both equations STEP #1: Put both equations in SAME FORM (Ax + By = C) STEP #2: SELECT A VARIABLE to eliminate (x or y) STEP #3: As needed, make that variable in both equations have same coefficients and opposite signs (ex: -3x and 3x) by MULTIPLIC ...
Partial differential equation

In mathematics, a partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (A special case are ordinary differential equations (ODEs), which deal with functions of a single variable and their derivatives.) PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, elasticity, or quantum mechanics. These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems. PDEs find their generalisation in stochastic partial differential equations.