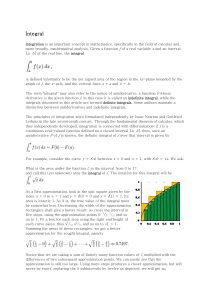
The Fundamental Theorem of Calculus.
... The FTC says that integration undoes differentiation (up to a constant which is irrevocably lost when taking derivatives), in the sense that Z x d (F (t))dt + C F (x) = a dt where C = F (a). The second part of the fundamental theorem says that differentiation undoes integration, in the sense that Z ...
... The FTC says that integration undoes differentiation (up to a constant which is irrevocably lost when taking derivatives), in the sense that Z x d (F (t))dt + C F (x) = a dt where C = F (a). The second part of the fundamental theorem says that differentiation undoes integration, in the sense that Z ...
Trigonometric Functions Key Words • Angle
... Initial Ray- The starting side of the angle. Terminal Ray- The ending side of the angle. Standard Position- The initial ray of the angle lies on the positive x axis. Degree- One 360 th of a circle. Radian- The length of the arc on a circle equal to the radius of the circle. Coterminal- Angles that h ...
... Initial Ray- The starting side of the angle. Terminal Ray- The ending side of the angle. Standard Position- The initial ray of the angle lies on the positive x axis. Degree- One 360 th of a circle. Radian- The length of the arc on a circle equal to the radius of the circle. Coterminal- Angles that h ...
Math 223 - Vector Calculus (Fall 2016) Homework 4
... 1. We need to write F as a gradient vector field to apply the Fundamental Theorem of Calculus for Line Integrals (FTOCLI). In other words we need to find a potential function f for F . Assume f (x, y , z) is such a function then F = grad f and we must have ∂f = y e xy ⇒ f = e xy + g(y , z). ∂x Diffe ...
... 1. We need to write F as a gradient vector field to apply the Fundamental Theorem of Calculus for Line Integrals (FTOCLI). In other words we need to find a potential function f for F . Assume f (x, y , z) is such a function then F = grad f and we must have ∂f = y e xy ⇒ f = e xy + g(y , z). ∂x Diffe ...