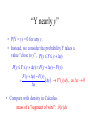Download Continuous Random Variables

Continuous Random Variables
Continuous Random Variables
• For discrete random variables, we required
that Y was limited to a finite (or countably
infinite) set of values.
• Now, for continuous random variables, we
allow Y to take on any value in some
interval of real numbers.
• As a result, P(Y = y) = 0
for any given value y.
CDF
• For continuous random variables,
define the cumulative distribution function
F(y) such that
F (Y )  P(Y  y),    y  
Thus, we have
lim F ( y )  0 and lim F ( y )  1
y 
y  
A Non-Decreasing Function
Continuous
random variable
Continuous distribution function
implies continuous random variable.
“Y nearly y”
• P(Y = y) = 0 for any y.
• Instead, we consider the probability Y takes a
value “close to y”, P( y  Y  y  y)
P( y  Y  y  y)  F ( y  y)  F ( y)
F ( y  y)  F ( y)

 y   F ( y ) dy, as y  0
y
• Compare with density in Calculus.
mass of a "segment of wire":  ( x)dx
PDF
• For the continuous random variable Y,
define the probability density function as
d[ F ( y)]
f ( y) 
 F ( y)
dy
for each y for which the derivative exists.
Integrating a PDF
• Based on the probability density function,
we may write
y
F ( y)   f (t )dt

Remember the 2nd Fundamental Theorem of Calc.?
Properties of a PDF
• For a density function f(y):
• 1). f(y) > 0 for any value of y.

• 2).  f (t )dt  P(Y  )  1
Problem 4.4
• For what value of k is the following function a
density function?
ky (1  y ), for 0  y  1
f ( y)  
otherwise
 0,
• We must satisfy the property



f (t )dt  P(Y  )  1
Exponential
• For what value of k is the following function a
density function?
 ke0.2 y , for 0  y
f ( y)  
otherwise
0,
• Again, we must satisfy the property



f (t )dt  P(Y  )  1
P(a < Y < b)
• To compute the probability of the event
a < Y < b ( or equivalently a < Y < b ),
we just integrate the PDF:
b
P(a  Y  b)  F (b)  F (a)   f (t )dt
a
5
F (5)  F (3)   f (t )dt
3
Problem 4.4
• For the previous density function
ky (1  y ), for 0  y  1
f ( y)  
otherwise
 0,
• Find the probability
P(0.4  Y  1)
• Find the probability
P(Y  0.4 | Y  0.8)
Problem 4.6
• Suppose Y is time to failure and

 1  e y , for y  0
F ( y)  
otherwise

0,
2
• Determine the density function f (y)
• Find the probability
P(Y  2)
• Find the probability
P(Y  1 | Y  2)