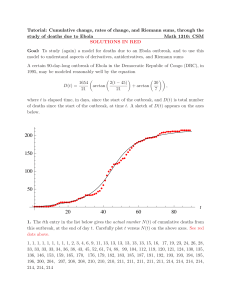
Geometry 15.09.16 CP1
... 1-4 Pairs of Angles In a circle a diameter is a segment that passes through the center of the circle and whose endpoints are on a circle. A radius of a circle is a segment whose endpoints are the center of the circle and a point on the circle. The circumference of a circle is the distance around th ...
... 1-4 Pairs of Angles In a circle a diameter is a segment that passes through the center of the circle and whose endpoints are on a circle. A radius of a circle is a segment whose endpoints are the center of the circle and a point on the circle. The circumference of a circle is the distance around th ...
Bird`s Eye View of Precalculus
... The sixth property is a consequence of the second property–check and see what happens if you let a = b. Also, the seventh property is a consequence of the second and sixth properties–check and see what happens when a = 0. 2) Functions and Composition. A function f (x) is even if f (−x) = f (x). The ...
... The sixth property is a consequence of the second property–check and see what happens if you let a = b. Also, the seventh property is a consequence of the second and sixth properties–check and see what happens when a = 0. 2) Functions and Composition. A function f (x) is even if f (−x) = f (x). The ...
Lecture10
... a) Recall that a random variable X is simply a function from a sample space S into the real numbers. The random variable is discrete is the range of X is finite or countably infinite. This refers to the number of values X can take on, not the size of the values. The random variable is continuous if ...
... a) Recall that a random variable X is simply a function from a sample space S into the real numbers. The random variable is discrete is the range of X is finite or countably infinite. This refers to the number of values X can take on, not the size of the values. The random variable is continuous if ...
Study Portfolio - New Paltz Central School District
... 2) A central angle of a circular garden measures 120 degrees and intercepts an arc of 90 feet. What is the radius of the garden measured to the nearest foot? ...
... 2) A central angle of a circular garden measures 120 degrees and intercepts an arc of 90 feet. What is the radius of the garden measured to the nearest foot? ...
∞ ∞ lnx sinx x =1 Local minimum
... Know how to approximate the area under a function by using the Left Sum, Right Sum and the Midpoint Sum (Example 1, WeBWorK 1) . Understand how the exact area is defined by taking the limit as the number of rectangles, n, approaches infinity (Example 3). Understand the distance problem: given the ve ...
... Know how to approximate the area under a function by using the Left Sum, Right Sum and the Midpoint Sum (Example 1, WeBWorK 1) . Understand how the exact area is defined by taking the limit as the number of rectangles, n, approaches infinity (Example 3). Understand the distance problem: given the ve ...